クラスに偏りがあるデータセットを使って、分類確率の閾値を変えることで、一方のクラスに分類されやすくします。
predict_probaでクラスの分類確率を見る
前回の投稿と同様に、kaggleで提供されているCredit Card Fraud Detectionデータセットをダウンロードして使います。
今回はロジスティック回帰で学習・テストさせてみます。
精度は99.92%ですが、クラスの偏りが極めて大きいため、混合行列を見ると陰性(不正利用ではない、クラス0)と判定されやすくなっています(偽陽性サンプル数は20なのに対して、偽陰性サンプル数は99)。
import pandas as pd from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix # CSVファイルをDataFrameへロード original_df = pd.read_csv('creditcard.csv') # 説明変数Xと目的変数yの抽出 X = original_df.loc[:, 'V1':'Amount'] y = original_df.loc[:, 'Class':] # 学習データとテストデータの分離 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0) # ロジスティック回帰で学習 lrc = LogisticRegression(random_state=0) lrc.fit(X_train, y_train) # スコアと混合行列 print('Train score: {:.4f}'.format(lrc.score(X_train, y_train))) print('Test score: {:.4f}'.format(lrc.score(X_test, y_test))) print('Confusion matrix:\n{}'.format(confusion_matrix(y_test, lrc.predict(X_test)))) # Train score: 0.9992 # Test score: 0.9992 # Confusion matrix: # [[142141 20] # [ 99 144]]
sklearn.linear_model.LogisticRegressionでは、各クラスに属する確率がサンプル毎に取得できるpredict_probaメソッドが提供されています。
例えば以下の場合、1つ目のサンプルがクラス0(不正利用でない)に分類される確率が0.999398754、クラス1(不正利用である)に分類される確率が0.00061246232となります。
lrc.predict_proba(X_test) # array([[ 9.99398754e-01, 6.01246232e-04], # [ 9.99651994e-01, 3.48005500e-04], # [ 9.99654291e-01, 3.45709049e-04], # ..., # [ 9.99226384e-01, 7.73615876e-04], # [ 9.99736105e-01, 2.63895411e-04], # [ 9.99347665e-01, 6.52334777e-04]])
2クラス分類の場合、サンプルの分類確率が0.5を以上のクラスで分類されます(クラス0の確率が0.6、クラス1の確率が0.4のサンプルは、クラス0と予測されます)。
この閾値を変えることで、一方のクラスをより分類されやすくなるように操作できます。 例えば下記のように閾値を0.3にすると、0.3より大きければクラス1に分類されるようになり、先程の結果よりも偽陰性が減少(99→82)していることがわかります(一方で偽陽性は20から36まで増えています)。
# 閾値を0.3に設定 y_pred = (lrc.predict_proba(X_test)[:, 1] > 0.3).astype(int) print('Confusion matrix:\n{}'.format(confusion_matrix(y_test, y_pred))) # Confusion matrix: # [[142125 36] # [ 82 161]]
適合率-再現率曲線を描く
では、この閾値をどうやって決めれば良いでしょうか。
この閾値を少しずつ変化させ、ある閾値の時の適合率(precision: 真陽性数/(真陽性数+偽陽性数))と再現率(recall: 真陽性数/(真陽性+偽陰性数))を計算するツールとして、sklearn.metrics.precision_recall_curveが提供されています。
x軸を適合率、y軸を再現率として、閾値による変化をプロットしてみます(適合率-再現率曲線)。
import numpy as np from sklearn.metrics import precision_recall_curve # ある閾値の時の適合率、再現率の値を取得 precision, recall, threshold = precision_recall_curve(y_test, lrc.predict_proba(X_test)[:, 1]) # 0から1まで0.05刻みで○をプロット for i in range(21): close_point = np.argmin(np.abs(threshold - (i * 0.05))) plt.plot(precision[close_point], recall[close_point], 'o') # 適合率-再現率曲線 plt.plot(precision, recall) plt.xlabel('Precision') plt.ylabel('Recall') plt.show()
プロットされた図を見ると、左上(閾値0.00の時は再現率100%)から右下(閾値1.00の時は適合率100%)に向かっており、閾値が高くなると、再現率が下がって適合率が上がる、というトレード・オフの関係が見えます。 適合率・再現率のバランスが良さそうな点は0.05(左上から2つ目の○)〜0.10(左上から3つ目の点)にありそうです。
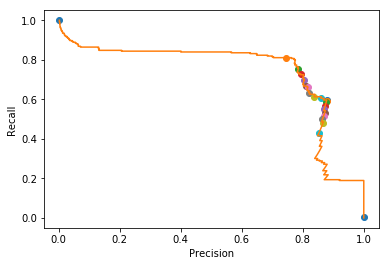
閾値を0.1に変えてみますと、偽陰性数は61まで減少しました。 (こういった閾値の調査は、他のハイパーパラメータ同様、本来は学習・テストとは異なるサンプルを使うべきです。)
y_pred = (lrc.predict_proba(X_test)[:, 1] > 0.1).astype(int) print('Confusion matrix:\n{}'.format(confusion_matrix(y_test, y_pred))) # Confusion matrix: # [[142111 50] # [ 61 182]]