Python: foliumでJupyter Notebookに地図を描画する

Jupyter Notebook上で、緯度経度の情報を地図へ簡単にプロットできる方法を探していたところ、foliumの使い勝手が良かったので紹介します。

folium

PythonからLeaflet.jsで地図をプロットするパッケージです。

https://github.com/python-visualization/folium

使用前にpip install foliumまたはconda install foliumでインストールします。

地図を表示する

まずは、千葉県千葉市の地図を表示します。

Mapで生成できます。

• locationオプションに中心の緯度・経度を渡しています
• Mapインスタンスを出力すると、leaflet.jsが読み込まれて表示されます
• デフォルトではOpenStreetMapの地図が使われます(tilesオプションでMapboxやStamenにも変更できます)
• zoom_startで表示する時のズームを変えられます(デフォルト10で、大きくするとより拡大されます)

import folium

chiba_map = folium.Map(location=[35.607451, 140.106340])

chiba_map

マーカをプロットする

次に千葉県の4つの市にマークします(緯度経度は市役所所在地、人口は千葉県のサイトから2018/1/1時点のデータを参照)。

市	緯度	経度	人口
千葉市	35.607451	140.106340	975,535
館山市	34.996596	139.869906	46,349
銚子市	35.734795	140.826926	61,674
浦安市	35.653146	139.902058	168,169

Markerで地図上にマーカをプロットできます。

• popupオプションで、マーカをクリックした時表示されるテキストを設定できます
• add_toメソッドでマップ上にプロットします

import pandas as pd

chiba_cities = pd.DataFrame({
    'city': ['千葉市', '館山市', '銚子市', '浦安市'],
    'latitude': [35.607451, 34.996596, 35.734795, 35.653146],
    'longtude': [140.106340, 139.869906, 140.826926, 139.902058],
    'population': [975535, 46349, 61674, 168169]
})

chiba_map = folium.Map(location=[35.607451, 140.106340], zoom_start=9)

for i, r in chiba_cities.iterrows():
    folium.Marker(location=[r['latitude'], r['longtude']], popup=r['city']).add_to(chiba_map)
    
chiba_map

マーカはいくつか種類があります。

CircleMarkerを使って、人口比を可視化してみます。

緯度経度を含む情報をぱぱっと可視化したいときに便利でしたので紹介しました。

GeoJSONを描画することもできます。詳しくはこちらの方の記事が参考になるかと思います。

国土数値情報とfoliumで市区町村区切りのコロプレス図を描く

Pythonで実装しながら緑本を学ぶ (第8章 マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデル)

データ解析のための統計モデリング入門(通称、緑本)を読み進めています。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第8章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter8.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

8 マルコフ連鎖モンテカルロ(MCMC)法とベイズ統計モデル

第7章では、ランダム効果を組み込んだ最尤推定を行いましたが、発生源が増えるとその分だけ多重積分が必要となり、計算が困難になります。

この章では、観測されたデータからある確率分布に従うランダムサンプルを取得するマルコフ連鎖モンテカルロ法(MCMC)と、パラメータを確率分布で表現するベイズ統計学を導入することで、上の問題を解くための準備をします。

8.1 例題：種子の生存確率(個体差なし)

架空植物20個体の種子8個の生死を調べることを想定する(第6章と同じ)。

(生存)種子数 が二項分布に従うと仮定すると、ある個体iの種子数が の確率と、尤度L(q)および対数尤度 は以下の式で計算されます。

$$ p(y_i \mid q)={}_8\mathrm{C}_{y_i}q^{y_i}(1-q)^{8-y_i} $$

$$ L(q)=p({\bf x} \mid q)=\prod_i p(y_i \mid q) $$

$$ \log L(q)=\sum_i {y_i \log q + (8-y_i) \log(1-q)}+\mbox{定数} $$

となるqを求めると、 と推定されます。なおこのデータは で生成されています。

8.2 ふらふら試行錯誤による最尤推定

上のように解析的に を求められない場合に、最尤推定を行なう方法を検討します。

非効率ですが1つの方法として、qを増減させながら、対数尤度が最大となる を逐次的に探索するアルゴリズムが考えられます。

1. qを離散化する
   • 例えば、0.01から0.99まで0.01刻みの値とする
2. スタート地点として、適当なqを選択して、その地点の対数尤度を求める
   • q=0.30において-46.38
3. qの両隣の点からランダムに選択して、 とする
   • または が選択される(それぞれ選択される確率は0.5)
4. における対数尤度を求める
   • で-47.62、 で-45.24
5. の方の対数尤度が大きければ、qを で更新する
   • なら更新せず、 ならqを0.31で更新する
6. 試行回数(例えば100回)だけ、3〜5を繰り返す

6.の指定回数を十分大きくすれば、やがて対数尤度が最大となる で収束することがイメージできるかと思います。

先程のデータに対して、上のアルゴリズムで最尤推定した結果が以下となります。
スタート地点が0.3でも0.6でも、 で安定していることがわかります。

8.3 MCMCアルゴリズムのひとつ：メトロポリス法

8.2の最尤推定アルゴリズムの手順5.に、以下の追加ルールを設けることで、MCMCのメトロポリス法となります。

• の対数尤度の方が小さい場合でも、確率rでqを で更新する

この確率rは、qと の尤度比です。

$$ r=\frac{L(q_{new})}{L(q)}=\exp(\log L(q_{new}) - \log L(q)) $$

この変更により、対数尤度が悪くなる場合であっても、確率rでqが更新されるようになります(対数尤度が良くなる場合は、常に で更新されます)。
Pythonでは以下のような実装となります。

# 対数尤度
def loglikelihood(data, q):
    ll = 0
    
    for i, r in data.iterrows():
        ll = ll + math.log(scipy.misc.comb(r['N'], r['y'])) + r['y']*math.log(q) + (r['N'] - r['y'])*math.log(1 - q)
        
    return ll

# MCMC(メトロポリス法)
def mcmc_metropolis(data, q_start, number_of_samples):
    q_current = q_start
    ll_current = loglikelihood(data, q_current)
    
    q = [q_current]
    ll = [ll_current]
    
    for r1, r2 in zip(np.random.random(number_of_samples), np.random.random(number_of_samles)):
        q_new = q_current + 0.01 if r1 > 0.5 else q_current - 0.01
        if q_new <= 0.01:
            q_new = 0.02
        elif q_new >= 0.99:
            q_new = 0.98
        ll_new = loglikelihood(data, q_new)
        
        # 対数尤度が悪くなる場合でも、尤度比の確率でqを更新
        if ll_current < ll_new or (math.exp(ll_new - ll_current)  > r2):
            q_current = q_new
            ll_current = ll_new
            
        q.append(q_current)
        ll.append(ll_current)
    
    return q, ll

# サンプル数100のMCMCでqと対数尤度の遷移を計算
q_100, ll_100 = mcmc_metropolis(data, 0.3, 100)

試行回数(MCMCではサンプリング数と呼ぶ)を100、1000、100000とした時の、それぞれのqの遷移を見てみます。 100回程度では最尤推定値までまだまだ遠く、また最尤推定値に到達後も変動することがわかります。

qの度数からqの確率分布が得られます。サンプリング数を十分大きくし、増やしても変動しなくなった時の確率分布を、マルコフ連鎖の定常分布( )とする)と呼びます。
サンプル1000回と100000回の確率分布を比較します。1000回の方が偏りが大きく、またスタート地点( )に引きずられてピークが左側にあることがわかります。

どのようなqからスタートしても最終的には定常分布 に従うが、サンプリング数は十分大きくする必要があります。ナイーブなメトロポリス法にはいくつか改善ポイントがあります。

• あるステップとその次のステップでサンプルされる値の相関が低いアルゴリズムを選ぶ
• (でたらめに選んだスタート地点の影響が強い)サンプリングの最初部分の値を捨てる
• 異なるスタート地点を選んだ複数のサンプリングを足し合わせる

qが0.1, 0.3, 0.6, 0.9からスタートした場合の動きを見てますと、いずれの場合もサンプル数が増えると0.45に近づくことがわかります。

定常分布 は尤度 に比例する確率分布です( は定数と見るため)。つまり、十分に長いMCMCサンプルは、メトロポリス法の定常分布 からのランダムサンプルとなります。

$$ p(q \mid {\bf Y})=\frac{L(q)}{\sum_q L(q)} $$

8.4 MCMCサンプリングとベイズ統計モデル

これまでGLMで推定してきたパラメータは、ただ1つに定まる値でした(統計学の枠組みでは頻度主義と呼ばれます)。

一方で、(上で求めたqのように)パラメータはある確率分布に従うものと表現されるものは、ベイズ統計学と呼ばれます。

上の例題をベイズ統計学で捉え直します。ベイズ統計学では、ベイズの公式で推論する統計学です。

$$ p(q \mid {\bf Y})=\frac{p({\bf Y} \mid q)p(q)}{\sum_q p({\bf Y} \mid q)p(q)} $$

• は、データ が得られた時にqが従う確率分布(事後分布)
• は、qの値の時にデータ が観測される確率
  • 二項分布の積である尤度が対応するので、
• はデータ が無い時のqの確率分布(事前分布)
  • 離散一様分布だろうか？(後の章の問題とする)
• は、条件付き確率の和なので、 で、qが不明の時にデータ が得られる確率(定数)

なので、ベイズの公式を以下のように変形できます。 もし事前分布 がqによらない定数なら、メトロポリス法で得られた と一致することがわかります。

$$ p(q \mid {\bf Y})=\frac{L(q)p(q)}{\sum_q L(q)p(q)} $$

8.5 補足説明

8.5.1 メトロポリス法と定常分布の関係

メトロポリス法で得られたqのサンプルが、定常分布 からのランダムサンプルであるためには、2つの条件を満たす必要がある。

• qが任意の初期値から定常分布 に収束すること
• あるqが に従っていて、次に得られた も に従っていること

8.5.2 ベイズの定理

先に登場した下式は、ベイズの定理と呼ばれます。

$$ p(q \mid {\bf Y})=\frac{p({\bf Y} \mid q)p(q)}{\sum_q p({\bf Y} \mid q)p(q)} $$

元々は条件付き確率と同時確率の関係を整理した、 という定義です。
、 の関係を使うことで、上の式を導出しています。

$$ p(q \mid {\bf Y})=\frac{p(q, {\bf Y})}{p({\bf Y})}=\frac{p({\bf Y} \mid q)p(q)}{p({\bf Y})}=\frac{p({\bf Y} \mid q)p(q)}{\sum_q p({\bf Y} \mid q)p(q)} $$

Pythonで実装しながら緑本を学ぶ (第7章 一般化線形混合モデル(GLMM))

データ解析のための統計モデリング入門(通称、緑本)を読み進めています。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第7章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter7.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

7 一般化線形混合モデル(GLMM) -個体差のモデリング-

GLMでは、説明変数が同じであれば、それ以外の要素は全て均質(=1つの平均λに定まる)という前提を置いている。
しかし、現実にはそうではなく、定量化できていない(原因不明の)個体間の差異がある。
この個体間のばらつきを、データのばらつきとは別の確率分布で表現するようにGLMを拡張したモデルが、一般化線形混合モデル(GLMM)です。

7.1 例題：GLMでは説明できないカウントデータ

架空植物100個体について葉数x(2〜6枚)から種子数y(0〜8個)を予測するモデルを想定する。

• 応答変数yが上限のあるカウントデータなので、第6章で扱った二項分布に従うと仮定する
• 線形予測子 、ロジットリンク関数で最尤推定する

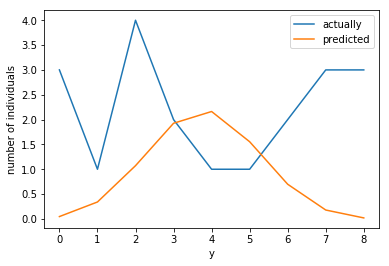
しかし、現実のデータはきれいな二項分布に従うとは限らない。x=4の時の分布(個体数20)を見てみると、谷のような形になることもありうる。

7.2 過分散と個体差

現実のデータは上のように、確率分布が仮定しているよりも、分散が大きくなる(過分散)の傾向が見られる。

x=4において、平均4.05であるのに対して、分散8.37となっており、二項分布が期待する分散2(=8×(4.05/8)×(1-(4.05/8)))よりもかなり大きい。

data4 = data[(data['x']==4)]

print('平均:', data4['y'].mean()) # 4.05
print('分散:', data4['y'].var()) # 8.37

データとして識別も定量化もされていない個体差があるため、こうした過分散が起こります。
しかし、個体差を全て特定し、定量化することは不可能です。そのため、これら原因不明の個体差の及ぼす影響を取り込んだ統計モデルが必要です。

7.3 一般化線形混合モデル

個体差の効果をGLMに取り込んだモデルが、一般化線形混合モデル(GLMM)です。

上の線形予測子に、個体iの個体差を表現するパラメータ (-∞〜+∞)を追加する(生存確率は では高く、 では低く補正されます)。
個体差 などのランダム効果(random effects)を線形予測子に含むため、"混合"と呼ばれます( や は固定効果(fixed effects)と言います)。

$$ logit(q_i)=\beta_1+\beta_2 x_i+r_i $$

GLMMでは個体差 はある確率分布に従うと仮定します。

ここでは平均0・標準偏差sの正規分布に従い、また、個体間で相互に独立した確率変数(独立同分布に従う)であると仮定します。確率密度関数 は以下のようになります。

$$ p(r_i \mid s)=\frac{1}{\sqrt{2 \pi s^2}}\exp(-\frac{r_i^2}{2s^2}) $$

rが小さいほど均質な集団、大きくなるほど個体差が大きい集団というふうになります。

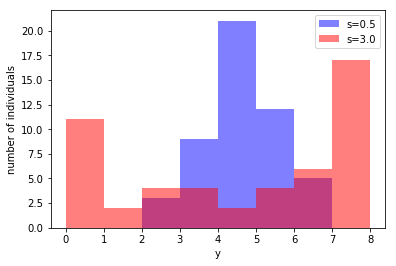
個体差のみから確率 を計算するモデル(下式)で、50個体の生存種子数をシミュレーションした図を示します。
s=0.5(青)の時の標本分散1.04だったのに対して、s=3.0(赤)では9.72となり、分布がかなりばらついていることがわかります。

$$ q_i = \frac{1}{1+\exp(-r_i)} $$

7.4 一般化線形混合モデルの最尤推定

個体差 はそのままでは最尤推定できません。

最尤推定して が得られたとしても、100個のデータに対して100個のパラメータを当てはめたフルモデルになるからです。

一方で、 と を推定するには、 を除いた式にする必要があります。そのために、 で積分することで を消します。

$$ L_i = \int_{-\infty}^{\infty} p(y_i \mid \beta_1, \beta_2, r_i) p(r_i \mid s) dr_i $$

式を見ると、左の項( )は二項分布、右の項( )は正規分布になっています。二項分布の項は 毎に異なるパラメータとなる(つまりサンプルサイズの数だけ二項分布がある)ため、かけあわせることで過分散な確率分布を作り出すことができる。

全データの尤度は100個体分の積となります。 はもうありません。最尤推定では を計算します。

$$ L(\beta_1, \beta_2, s)=\prod_i L_i $$

PypeRでPythonからRを実行する

さて、RではglmmMLパッケージで簡単にGLMMの最尤推定ができます。
しかし、PythonではGLMMで最尤推定を計算するライブラリというのは無く、statsmodelsやPyStanでも実装されていないようです。(さらに複雑化したモデルにも対応できるベイズモデルが既に実装・提供されているからでしょうか。)

そこで、タイトルと異なっていて不本意ではありますが、PythonからRのコードを実行するPypeRを導入します。以降のコードは実行環境にRがインストールされている前提となります。

http://bioinfo.ihb.ac.cn/softwares/PypeR/

まずはpyper.Rオブジェクトを作成します。

import pyper # pip install pyper

r = pyper.R()
type(r) # pyper.R

得られたRオブジェクトを、r("実行したいRコード")のように関数形式で呼び出すことで、Rのコードが実行されます。
assignメソッドを使うことで、Pythonのオブジェクトを任意の名前でRに渡すこともできます。PandasのDataFrameやSeriesもそのまま渡せます。

r.assign("data", data)

print(r("summary(data)"))
# try({summary(data)})
#        N           y              x           id        
#  Min.   :8   Min.   :0.00   Min.   :2   Min.   :  1.00  
#  1st Qu.:8   1st Qu.:1.00   1st Qu.:3   1st Qu.: 25.75  
#  Median :8   Median :3.00   Median :4   Median : 50.50  
#  Mean   :8   Mean   :3.81   Mean   :4   Mean   : 50.50  
#  3rd Qu.:8   3rd Qu.:7.00   3rd Qu.:5   3rd Qu.: 75.25  
#  Max.   :8   Max.   :8.00   Max.   :6   Max.   :100.00  

それでは、glmmMLパッケージで最尤推定を行います。事前に> install.packages("glmmML")でインストールしておきます。

glmmMLの引数を見ると、GLMで渡したパラメータに加えて、cluster = idが渡されています。clusterは個体ごとに異なるパラメータを期待しており、今回は個体ごとに異なる通し番号を渡しています。

r("""
library(glmmML)
result <- glmmML(cbind(y, N-y) ~ x, data = data, family = binomial, cluster = id)
"""))

推定した結果をPythonのオブジェクトに戻す時は、getメソッドを使います。

result = r.get("result")

print(result)

resultオブジェクト(dict)には、以下の値を持っていました。

• coefficientsに最尤推定値が格納されており、 、 とそれぞれ推定されています
• sigmaに分散で、2.408となっています
• AICは275(残差は269)

{'aic': 275.414,
 'boot': 0,
 'bootP': None,
 'call': array(['glmmML', 'cbind(y, N - y) ~ x', 'binomial', 'data', 'id'],
       dtype='<U19'),
 'cluster.null.deviance': 513.836,
 'cluster.null.df': 98,
 'coef.sd': array([ 0.878,  0.207]),
 'coefficients': array([-4.19 ,  1.005]),
 'converged': True,
 'deviance': 269.414,
 'df.residual': 97,
 'info': 0,
 'posterior.modes': array([-1.337,  0.195,  0.967,  2.007,  0.195, -1.337, -1.337,  3.556,
         0.195,  2.962, -1.337, -1.337, -1.337, -1.337, -1.337,  0.195,
         1.526,  2.469,  1.526,  3.556,  0.069, -0.648, -1.951,  2.05 ,
        -0.648,  0.069, -1.951, -1.951, -1.951,  0.608,  1.546,  1.546,
        -1.951, -1.951, -1.951,  3.639,  1.082,  0.069, -1.951,  3.639,
         1.142, -0.834, -2.638,  0.624,  1.142, -0.834,  2.884, -0.834,
         1.801,  1.801,  2.884, -2.638,  0.157,  1.801, -0.312, -1.507,
        -0.312, -0.834,  2.884, -2.638,  0.938, -0.768, -1.742, -1.233,
        -1.233,  0.938,  2.177,  0.938, -3.378,  0.938,  2.177,  2.177,
         2.177,  0.237,  0.938, -0.768, -0.296, -2.376,  2.177, -1.742,
        -3.256, -3.256, -4.158,  1.536,  1.536,  1.536,  1.536,  1.536,
         1.536,  1.536,  1.536, -4.158, -0.663, -2.156, -2.156,  0.089,
        -1.215,  0.089, -2.653,  1.536]),
 'prior': 'gaussian',
 'sigma': 2.408,
 'sigma.sd': 0.220,
 'terms': array(['~', 'cbind(y, N - y)', 'x'],
       dtype='<U15'),
 'variance': array([[  7.703e-01,  -5.691e-04,  -1.456e-03],
        [ -5.691e-04,   4.304e-02,   1.181e-02],
        [ -1.456e-03,   1.181e-02,   4.849e-02]])}

7.5 現実のデータ解析にはGLMMが必要

GLMとGLMMの使い分けは「同じ個体から採取されているか」にかかっており、「全て異なる個体から採取している(反復と呼ばれます)」場合はGLM、「同じ個体から採取している(疑似反復と呼ばれます)」場合はGLMMを適用すべき。

ある個体から1回しか採取されない場合は、個体差がわからないので変数化する必要はありません。そのため線形予測子は固定効果の変数のみを持ちます。

$$ logit(q_i) = \beta_1 + \beta_2 x_i $$

しかし、同じ個体iから複数回採取する場合は、個体差が識別できるので変数化( )してモデルに加える必要があります。

$$ logit(q_i) = \beta_1 + \beta_2 x_i + r_i $$

さらに各個体が存在する場所jが異なっており、それぞれの場所にある個体から複数回採取されている、といったケースでは、さらにその場所も変数( )として加えます。

$$ logit(q_i) = \beta_1 + \beta_2 x_i + r_i + r_j $$

こうしてランダム効果が複数の変数で表現されると、最尤推定で多重積分する必要があります。このようなときには、代わりに階層ベイズモデルとMCMCが組み合わせた方法が使われます(第8章以降のテーマ)。