2018-01-25

Pythonで実装しながら緑本を学ぶ (第3章一般化線形モデル(GLM))

Python 統計学読書メモ

データ解析のための統計モデリング入門(通称、緑本)を読み始めました。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第3章です(前回の投稿はこちら)。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter3.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

3 一般化線形モデル(GLM)

個体ごとに異なる説明変数によって応答変数が変化する統計モデルとしてポアソン回帰を導入する。ポアソン回帰は一般線形化モデル(GLM)の一つです。

この章では2つのデータを使います。
1つは、第3章で扱われている架空植物100個体の種子数のデータで、著者サイトから入手できます。目的変数は種子数(y)です。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html
もう1つは、前回の投稿でも使いました、UCIで提供されているStudent Performance Data Setです。目的変数は欠席数(absences)です(前回同様、外れ値の除去や、欠席2回を1回とカウントするなど、若干の前処理を行っています)。
https://archive.ics.uci.edu/ml/datasets/student+performance

この投稿では種子数データ、欠席数データとそれぞれ呼ぶことにします。

3.1 例題: 個体ごとに平均種子数が異なる場合

種子数データでは、以下の個体差がある架空の植物100個体を想定している。個体差はいずれも観測データとして与えられている。平均種子数に影響を与えているのかについて知りたい。

体サイズ $x_i$
施肥処理の有無(50個体は施肥処理有り) $f_i$

f:id:ohke:20180125211542p:plain

また、欠席数データでは、以下の特徴(個体差)を持つ生徒389人に対して、欠席数(absences)との関係を調べます。

年齢 (age)
恋人がいるかどうか (romantic)

f:id:ohke:20180125211612p:plain

3.2 観測されたデータの概要を調べる

Pandasでデータの概要を見る場合は、head()で先頭5行、info()でデータの型、value_counts()で値の分布、describe()で要約統計量をそれぞれ出力すると良いかと思います。

# 先頭5行の表示
data.head()

# 各列の型
data.info()

# fの値の分布
data['f'].value_counts()

# 数値列(x列とy列)の要約統計量
data.describe()

3.3 統計モデリングの前にデータを図示する

散布図と箱ひげ図でデータの分布を視覚化します。

種子数データでは、散布図では体サイズが大きくなるほど種子数も増える傾向が見られますが、箱ひげ図からは施肥処理による種子数の変化は読み取れません。

# 散布図
plt.scatter(data[data['f']=='C']['x'], data[data['f']=='C']['y'], marker='o', label='C')
plt.scatter(data[data['f']=='T']['x'], data[data['f']=='T']['y'], marker='x', label='T')
plt.legend(loc='best')
plt.show()

f:id:ohke:20180124092516p:plain

# 箱ひげ図
fig, ax = plt.subplots()
ax.boxplot([data[data['f']=='C']['y'], data[data['f']=='T']['y']])
ax.set_xticklabels(['C', 'T'])
plt.show()

f:id:ohke:20180124092533p:plain

次に欠席数データについて見てみます。

散布図では、17歳をピークとした山になっていますが、概ね年齢が上がると欠席数も増える傾向がありそうです。箱ひげ図では、恋人がいる方が欠席数は多くなることが伺えます。

f:id:ohke:20180125142237p:plain

f:id:ohke:20180125142247p:plain

3.4 ポアソン回帰の統計モデル

個体iの種子数 $y_i$ がポアソン分布に従っていると仮定します。

$p(y_i\mid\lambda_i)=\frac{\lambda_i^{y_i}exp(-\lambda_i)}{y_i !}$

個体ごとに異なる平均 $\lambda_i$ を説明変数(共変量) $x_i$ の関数として、仮に以下で定義する。 $\beta_i$ はパラメータ(係数)と呼び、当てはまりの良い値を選ぶ。

$\lambda_i=\beta_i+\beta_2 x_i \Leftrightarrow \log\lambda_i=\beta_1+\beta_2 x_i$

右辺 $\beta_1+\beta_2 x_i$ は、線形予測子
左辺の関数は、リンク関数
- 対数( $\log\lambda_i$ )の場合は、対数リンク関数と呼ばれ、ポアソン分布に使われる
- 対数リンク関数、ロジットリンク関数(ロジスティック回帰で用いる)は、正準リンク関数と呼ばれる

当てはまりの良さは対数尤度関数で定量化し、対数尤度が最大となる $\hat{\lambda_i}$ を求めていましたが、それを今回導入したパラメータの関数に置き換えます。以下の関数を最大にする ${\beta_1, \beta_2}$ を求めます。

$\log L(\beta_1,\beta_2)=\sum_i\log\frac{\lambda_i^{y_i}exp(-\lambda_i}{y_i !}$

最尤推定量は、Rだと> fit <- glm(y ~ x, data = d, family = poisson)で求められますが、PythonではstatsmodelやPyStanでこうした計算が簡単に行なえます。今回はstatsmodelを使います。

http://www.statsmodels.org/stable/index.html

以下のコードではいずれも最尤推定を計算しています。実行前にstatsmodelsをインストール( pip install statsmodels )する必要があります。
statsmodelsには2種類のAPI(statsmodels.apiとstatsmodels.formula.api)があります。statsmodels.apiでは説明変数と目的変数を受け取るピュアな関数が提供されます。一方、statsmodels.formula.apiでは目的変数と説明変数の関係式をRのフォーマットで渡せます。

import statsmodels.api as sm

# 最尤推定(切片も含む場合はadd_constant()で値を渡す)
results = sm.Poisson(data['y'], sm.add_constant(data['x'])).fit()
#results = sm.GLM(data['y'], sm.add_constant(data['x']), family=sm.families.Poisson()).fit()
# 結果の出力
results.summary()

import statsmodels.formula.api as smf

# 最尤推定
results = smf.poisson('y ~ x', data=data).fit()
# 結果の出力
results.summary()

結果は以下のように出力されます。

最尤推定値(coef)はそれぞれ、 (Interceptまたはconst)は1.2917、 (x)は0.0757
- 標準誤差(std err)は、最尤推定値のばらつき
- z値(z value)は、最尤推定値÷標準誤差で、推定値が0から十分離れていることの目安
- Pr|>z|は、マイナス無限大から0までの値をとる確率
このときの最大対数尤度(Log-Likelihood)は-235.39

f:id:ohke:20180120160400p:plain

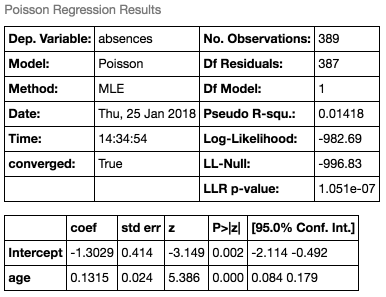
同様に、欠席数データに対しても適用すると、以下の結果になります。
最尤推定値(coef)は、 $\hat{\beta_1}$ (Intercept)は-1.3029、 $\hat{\beta_2}$ (age)は0.1315で、このときの最大対数尤度は-982.69です。第2章のモデルの最大対数尤度は-996.83( $\lambda=2.47$ の時)だったので、それよりも当てはまりの良いモデルとなっていることがわかります(ちなみに $\lambda$ が一定のモデルの最大対数尤度はLL-Nullの値と一致します。第4章で詳しく見ていきます)。

f:id:ohke:20180125195640p:plain

3.5 説明変数が因子型の統計モデル

施肥処理の有無を表す $f_i$ のように、Rでは数量型以外で特定の値(水準)をとる変数を因子型と言います。因子型の場合は、ダミー変数に置き換えてモデル化します。

施肥処理の効果のみを考慮した以下のモデルでは、 $d_i$ がダミー変数ですが、 $f_i=C$ の時は $d_i=0$ 、 $f_i=T$ の時は $d_i=1$ となるようにします。

$\lambda_i=exp(\beta_1+\beta_3 d_i)$

pandasではget_dummies()でダミー変数に置き換えることができます。

# f=Tの場合に1となる列d(ダミー変数)を追加
data['d'] = pd.get_dummies(data['f'])['T']

結果は以下のとおりです。
0か1しか値を持たないにもかかわらず、最尤推定値は0.0128と小さな値となっていることから、種子数に対する影響は小さいことがわかります。

f:id:ohke:20180125195640p:plain

欠席数データに対しても、恋人の有無をダミー変数に置き換えたモデルを作りました。
こちらは、最尤推定値が0.2250でそれなりに影響力はありそうです。

f:id:ohke:20180125200930p:plain

3.6 説明変数が数量型＋因子型の統計モデル

複数の説明変数を組み合わせる場合は、線形予測子で和として表現する。

$\log\lambda_i=\beta_1+\beta_2 x_i+\beta_3 d_i$

Pythonでも単純で、'y ~ x+d'と表現できます。

results = smf.poisson('y ~ x+d', data=data).fit()

種子数データの結果を見ると、fはマイナスの推定値となっており、種子数については逆効果となりそうです。一方、最大対数尤度は少し良くなっています。

f:id:ohke:20180125205112p:plain

得られた最尤推定値を当てはめると、 $\lambda_i$ は以下の式で導出されます。logが取り払われたことで、乗算で $\lambda_i$ に影響を与えることがわかります。

$\lambda_i=exp(1.26+0.08x_i-0.032d_i)$

欠席数データでは、 $\lambda_i$ は以下の式になります。2変数となったことで、最大対数尤度も-979.35と良くなっています。

$\lambda_i=exp(-1.2045+0.1219\times age_i+0.1752d_i$

f:id:ohke:20180125205326p:plain

3.7 「何でも正規分布」「何でも直線」には無理がある

確率分布を等分散の正規分布、リンク関数を恒等リンク関数(何もしない、つまり $\lambda_i=\beta_1+\beta_2 x_i+\beta_3 d_i$ で表現される $\lambda_i$ )にすると、線形モデル(LM)と呼ばれる。

そのLMの1つが直線回帰です。直線回帰は以下の特徴を持つため、今回のカウントデータでは不適切といえる。

応答変数Yは平均で標準偏差ρの正規分布に従うと仮定
- 正規分布では連続値を扱う
- ばらつきも一定
平均値は
- 負の値をとり得る

応答変数にあわせて、確率分布は適切に選ぶべき。

2018-01-19

Pythonで実装しながら緑本を学ぶ (第2章確率分布と統計モデルの最尤推定)

Python 統計学

今回は第2章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter2.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

2 確率分布と統計モデルの最尤推定

2.1 例題：種子数の統計モデリング

著者・久保氏のサポートサイトから提供されているデータ(架空の植物50個体の種子数)を使って、要約値(最大・最小、標本平均、四分位数など)を表示しています。

私の実装では、UCIで提供されているStudent Performance Data Setを使いました。
データの詳細は以下ですが、その中でもカウントデータとなっている数学の欠席数を説明変数として取り上げます(生徒数389人、欠席数30以上の生徒は除外しています)。

https://archive.ics.uci.edu/ml/datasets/student+performance

zipファイルはzipfileモジュールで簡単に解凍できます。

import zipfile


# カレントディレクトリに解凍
zfile = zipfile.ZipFile('student.zip')
zfile.extractall('.')

PandasのDataFrameにロードして欠席数(absences)をヒストグラムに描くと、以下のようになりました。
なぜか奇数の分布が少ないことがわかります。数学の授業は2時間連続となっており、1日休むと2回欠席したことになる(欠席数1の人は遅刻して2時間目の授業から出席した)などが考えられます。

f:id:ohke:20180117085651p:plain

そこで2で割って切り捨てることで、欠席数0〜1の人は0回、2〜3の人は1回、・・・となるように整形し、再度ヒストグラムを描きました。
以降では、この値を使うこととします。

f:id:ohke:20180117084948p:plain

2.2 データと確率分布の対応関係をながめる

データに見られるばらつきを表すために、確率分布を導入する。

確率分布とは、確率変数の値とそれが出現する確率を対応させたものです。
確率変数は、今回の例では、ある生徒iの欠席数 $y_i$ のことで、生徒毎にばらつきのある変数です。したがって、例えば「 $y_i=1$ の発生確率はいくらか」「 $y_i=2$ の発生確率はいくらか」・・を表現するものが確率分布です。

欠席数データのヒストグラムに、平均2.47のポアソン分布を重ねた図が、以下となります。
漸近的な減少傾向はポアソン分布で表せているようですが、当てはまりはそこまで良くないようです(「当てはまり」の定量的な評価は、この後行います)。

f:id:ohke:20180117142048p:plain

Pythonでポアソン分布の擬似乱数を生成するには、numpy.randomのpoissonメソッドを使う方法とscipy.stats.poissonのrvsメソッドを使う方法の、2つがあります。
以下のコードはいずれも平均2.47のポアソン分布に従う擬似乱数10,000個を生成しています。

import numpy as np
from scipy.stats import poisson


# 平均2.47のポアソン分布に従う擬似乱数10,000個を生成
poisson_values = np.random.poisson(lam=2.47, size=10000)
poisson_values = poisson.rvs(2.47, size=10000)

2.3 ポアソン分布とは何か？

ポアソン分布は以下の式で表現される確率分布です。

$p(y \mid \lambda)=\frac{\lambda^{y}exp(-\lambda)}{y!}$

パラメータはλのみ
$y \in {0, 1, 2, ..., ∞}$ の値を取り、全てのyの総和が1となる
確率分布の平均はλ(λ≧0)
分散と平均は等しい
観測データ同士は独立し、相関や相互作用は無いという前提も置いている

λ∈{3.5, 7.7, 15.1}の3パターンのポアソン分布を以下のようになります。

f:id:ohke:20180118080332p:plain

あるポアソン分布における確率分布を計算するためには、scipy.stats.poissonのpmfメソッドを使います。

# 平均3.5のポアソン分布で、確率変数が0〜14の時の確率分布を計算
prod = [poisson.pmf(i, 3.5) for i in range(15)]
# [0.030, 0.106, 0.185, 0.216, 0.189, 0.132, 0.077, 0.039, 0.017, 0.007, 0.002, 0.001, 0.000, 0.000, 0.000]

欠席数データへのポアソン分布の当てはまりが悪く感じられたのは、平均と分散が近くない(平均2.47に対して分散7.95)ためと思われます。

print('平均: {}'.format(data.mean())) # 平均: 2.47
print('分散: {}'.format(data.var())) # 分散: 7.95

2.4 ポアソン分布のパラメーターの最尤推定

確率分布のパラメータ(ポアソン分布の場合はλ)を、観測データに基いて推定することを最尤推定(法)という。

最尤推定法は、当てはまりの良さを表す尤度を最大化するパラメータを探す。
ポアソン分布の尤度L(λ)以下の式で求められます(要するに「 $y_1$ である」かつ「 $y_2$ である」かつ・・・でN個の事象が同時に起こる確率を求めてます)。

$L(\lambda) = p(y_1 \mid \lambda) \times p(y_2 \mid \lambda) \times \dots \times p(y_N \mid \lambda) = \prod_{i}^{N}p(y_i \mid \lambda) = \prod_{i}^{N}\frac{\lambda^{y_i}exp(-\lambda)}{y_{i}!}$

アンダーフローを防ぐために、対数変換した対数尤度関数が使われます。

$\log L(\lambda)=\sum_i^N (y_i \log \lambda - \lambda - \sum_k^{y_i} \log k)$

λを0.5〜3.0まで0.01刻みで変化させた時の、欠席数データに対する対数尤度関数の値をプロットしました。λ=2.5付近で最大となることがわかります。

f:id:ohke:20180118084906p:plain

対数尤度関数が最大値となるλを最尤推定量といい、 $\hat{\lambda}$ とします。
$\hat{\lambda}$ は対数尤度関数の傾きが0となる点であるため、λで偏微分します。

$\frac{\partial L(\lambda)}{\partial\lambda}=\sum_i^N(\frac{y_i}{\lambda}-1)=\frac{1}{\lambda}\sum_i^{y_i}-N$

傾きが0の時、 $\hat{\lambda}$ は標本平均( $\frac{1}{N}\sum_i y_i$ )となります。

2.5 統計モデルの要点：乱数発生・推定・予測

モデルの良さは、そのモデルの予測の良さで決まる。

与えられた観測データがポアソン分布という仮定を置き、パラメータλを求めることが推定(あてはめ)と言う
推定で得られた統計モデルを使い、未知の観測データの分布を見積もることが予測

2.6 確率分布の選び方

確率分布は説明変数の性質に着目して選択する。

確率分布	離散 or 連続	範囲	標本分散と標本平均の関係
ポアソン分布	離散値	0以上(上限無し)	平均≒分散
二項分布	離散値	0以上で有限範囲	分散は平均の関数
正規分布	連続値	[-∞, +∞]	分散は平均と無関係
ガンマ分布	連続値	[0, +∞]	分散は平均の関数

2018-01-13

Python: レコメンドの行列分解を確率的勾配降下法で実装してMovieLens100Kに適用する

Python Recommender system

前々回の投稿( Python: レコメンドの行列分解を確率的勾配降下法で実装する - け日記 )では、欠測値やバイアスを考慮した行列分解を、確率的勾配降下法(SGD)で求める実装を行いました。

今回はおなじみMovieLens100K Datasetへ、このアルゴリズムを適用します。

MovieLens | GroupLens

性能の問題

前々回の投稿のおさらいです。

ohke.hateblo.jp

SGDでは以下の目的関数を最小化する4つのパラメータ( $b_u$ , $b_i$ , q, p)を求めていました。

$\min_{b, q, p} \sum_{(u, i) \in R} (r_{ui} - \mu - b_{i} - b_{u} - q^T_i p_u)^2 + \lambda (b_i^2 + b_u^2 + \mid q_i \mid ^2 + \mid p_u \mid ^2)$

評価値1つずつに対して、誤差の計算とパラメータの更新(下式)を行っていました。

$b_i \leftarrow b_i + \gamma (e_{ui} - \lambda b_i)$
$b_u \leftarrow b_u + \gamma (e_{ui} - \lambda b_u)$
$q_i \leftarrow q_i + \gamma (e_{ui} p_u - \lambda q_i)$
$p_u \leftarrow p_u + \gamma (e_{ui} q_i - \lambda p_u)$

このとき、 $e_{ui}$ の計算コストが問題となります。パラメータを更新するたびに、誤差 $e_{ui}$ も再計算しているためです。評価値が100,000個あれば誤差も100,000個あるため、1回の再計算のコストも大変高くなります。

実際、前々回の実装をそのままMovieLens100K Datasetに適用したところ、学習に時間がかかりすぎてしまいました。

ミニバッチの導入

そこで、ミニバッチを導入します。

ミニバッチ勾配降下法(MSGD、単にSGDとも)では、評価値1つずつに対して誤差の計算とパラメータの更新を行うのではなく、例えば100個ごとで誤差の計算とパラメータの更新をまとめて行います。これにより、誤差 $e_{ui}$ の計算回数が1エポックあたり100,000回から1,000回まで削減できます。
各種勾配降下法の比較については、こちらの投稿が参考になります。

勾配降下法の最適化アルゴリズムを概観する | コンピュータサイエンス | POSTD

確率的勾配降下法でパラメータを学習する関数sgd()を、ミニバッチを導入して書き直したmsgd()を作成します。それ以外の関数の実装は、前々回と同じです。

ミニバッチで一度に扱う評価値の個数を表すbatch_sizeを引数に追加
delta_bu, delta_bi, delta_q, delta_pにミニバッチ内での更新値が累積される

import numpy as np
import pandas as pd
import math
import time
import codecs
from scipy import sparse
from matplotlib import pyplot


def get_initial_values(x, k):
    # 各行列またはベクトルの値を、-0.05〜+0.05の乱数で初期化
    mu = np.sum(x) / np.count_nonzero(x)
    bu = (np.random.rand(x.shape[1]) - 0.5) * 0.1
    bi = (np.random.rand(x.shape[0]) - 0.5) * 0.1
    q = (np.random.rand(k, x.shape[0]) - 0.5) * 0.1
    p = (np.random.rand(k, x.shape[1]) - 0.5) * 0.1
    
    return (mu, bu, bi, q, p)


def get_error_matrix(x, mu, q, p, bu, bi):
    # 誤差eの計算
    return x - (mu + np.dot(q.T, p) + bu + np.matrix(bi).T)


def error_function(x, mu, q, p, bu, bi, l):
    # 誤差に正則化制約を加えた目的関数を定義
    error_matrix = get_error_matrix(x, mu, q, p, bu, bi)
    error = np.sum(np.square(error_matrix[x > 0]))
    
    regularization = l * (np.sum(np.square(bu)) + np.sum(np.square(bi)) + np.sum(np.square(q)) + np.sum(np.square(p)))
    
    return error + regularization


def msgd(x, k, epochs=100, l=0.02, gamma=0.02, batch_size=1):
    # 確率的勾配法で分解した行列とバイアスを求める
    mu, bu, bi, q, p = get_initial_values(x, k)
    errors = [] # エポック毎の目的関数の値
    
    for epoch in range(epochs):
        # 誤差の計算
        error = error_function(x, mu, q, p, bu, bi, l)
        errors.append(error)
        
        # 欠測値を除いた評価値のインデックスを取得してランダムに並び替える
        x_i, x_u = np.where(x > 0)
        rating_count = len(x_i)
        batch_count = math.ceil(rating_count / batch_size)
        targets = np.arange(rating_count)
        np.random.shuffle(targets)
        
        # ミニバッチ単位で誤差の計算とパラメータの更新を行う
        for batch_base in range(batch_count):
            error_matrix = get_error_matrix(x, mu, q, p, bu, bi)
            
            delta_bu = np.zeros_like(bu)
            delta_bi = np.zeros_like(bi)
            delta_q = np.zeros_like(q)
            delta_p = np.zeros_like(p)
            
            for batch_offset in range(batch_size):
                # 対象の評価値のインデックスを計算
                target_index = batch_size * batch_base + batch_offset
                i = x_i[target_index]
                u = x_u[target_index]
                e_ui = error_matrix[i, u]
                
                # パラメータの更新値を累積
                delta_bu[u] += gamma * (e_ui - l * bu[u])
                delta_bi[i] += gamma * (e_ui - l * bi[i])
                delta_q[:, i] += gamma * (e_ui * p[:, u] - l * q[:, i])
                delta_p[:, u] += gamma * (e_ui * q[:, i] - l * p[:, u])
                
            # パラメータの更新
            bu += delta_bu
            bi += delta_bi
            q += delta_q
            p += delta_p

    error = error_function(x, mu, q, p, bu, bi, l)
    print('Error: {}'.format(error))
    
    # 予測した評価値を生成
    expected = mu + bu + np.matrix(bi).T + np.dot(q.T, p)
    
    return expected, errors

MovieLens100K Datasetでの評価

今回もMovieLens 100K Datasetを使います。

以下からダウンロードして、今回作成するPythonファイルと同じディレクトリに解凍しておきます。以前の投稿( word2vecでitem2vecを実装して映画を推薦する - け日記 )も参考にしてみてください。

MovieLens | GroupLens

評価値はnumpy行列にして持ちます。欠測値は0で補完しています。アイテムIDとタイトルの一覧もDataFrameにロードしておきます。
また、指定したユーザに対して未評価のアイテムの評価値を予測してランキングを返すpredict_ranking()と、それを表示するprint_ranking()を実装しています。

# 評価値を持つファイルはu.data。楽に行列化するために、まずはDataFrameでロードする
ratings = pd.read_csv('ml-100k/u.data', delimiter='\t', header=None).iloc[:, :3]
ratings.rename(columns={0: 'user_id', 1: 'item_id', 2: 'rating'}, inplace=True)
print('ratings.shape: {}'.format(ratings.shape)) # ratings.shape: (100000, 3)

# item_idを行、user_idを列とする1682×943の行列(欠測値は0埋め)
rating_matrix = np.asmatrix(ratings.pivot(index='item_id', columns='user_id', values='rating').fillna(0), dtype=np.float64)
print('rating_matrix.shape: {}'.format(rating_matrix.shape)) # rating_matrix.shape: (1682, 943)

# pd.read_csvで読み込もうとすると文字コードエラーになるため、
# codecs.openでエラーを無視してファイルを読み込んだ後にDataFrameにする
with codecs.open('ml-100k/u.item', 'r', 'utf-8', errors='ignore') as f:
    item_df = pd.read_table(f, delimiter='|', header=None).ix[:, 0:1]
    item_df.rename(columns={0: 'item_id', 1: 'item_title'}, inplace=True)
    item_df.set_index('item_id', inplace=True)

items = pd.Series(item_df['item_title'])
print('items.shape: {}'.format(items.shape)) # items.shape: (1682, 1)


def predict_ranking(user_index, reducted_matrix, original_matrix, n):
    # 対象ユーザの予測評価値
    reducted_vector = np.array(reducted_matrix[:, user_index].T)[0]
    
    # 評価済みのアイテムの値は0にする
    filter_vector = np.array(original_matrix[:, user_index].T)[0] == 0
    predicted_vector = np.multiply(reducted_vector, filter_vector)

    # 上位n個のアイテムのインデックスを返す
    return [(i, predicted_vector[i]) for i in np.argsort(predicted_vector)[::-1][:n]]


def print_ranking(user_ids, items, reducted_matrix):
    for user_id in user_ids:
        print('User ID: {}'.format(user_id))
        predicted_ranking = predict_ranking(user_id - 1, reducted_matrix, rating_matrix, 10)
        for item_id, rating in predicted_ranking:
            # アイテムID, 映画タイトル, 予測した評価値を表示
            print('{}: {} [{}]'.format(item_id + 1, items[item_id + 1], rating))

それでは予測評価値の行列を作ります。

k(qとpの行サイズ)は30とし、これまでのSVDやNMFと同じ値に設定
エポック数は1000として、エポック毎に目的関数の値(誤差)をプロットすることで、十分低減できているかを確認
- 学習に約90分を要しました

# 1000エポックにして誤差の傾向を確認
%time reducted_matrix, errors = msgd(rating_matrix, k=30, epochs=1000, batch_size=1000, gamma=0.001)
# Error: 22387.638436133657
# CPU times: user 1h 22min 20s, sys: 19min 38s, total: 1h 41min 59s
# Wall time: 1h 29min 37s

エポック毎の目的関数の値をプロットしたグラフが以下です。
エポック数600を超えたあたりから大きな変化はないため、エポック数1000で十分と判断できます。最終的な誤差は22387となり、k=30ではこのくらいが限界と予想されます。

f:id:ohke:20180108132848p:plain

最後に、2人のユーザへ推薦させてみます。

SVDやNMFとの結果と比較するために、前回と同じ2人のユーザ(ユーザID 267と868)を対象にランキングを生成しました。この2人は"Akira(1988)"と"Ghost in the Shell(Kokaku kidotai)(1995)"を5で評価しています(つまりSF+アニメーション好きです)。

akira_item_id = 206
ghost_in_the_shell_item_id = 1240

# Akira (1988)とGhost in the Shell (Kokaku kidotai) (1995)を5で評価したユーザIDを取得
user_ids = np.where(np.multiply(rating_matrix[akira_item_id - 1] == 5, rating_matrix[ghost_in_the_shell_item_id - 1] == 5))[1] + 1

print_ranking(user_ids, items, reducted_matrix)

結果を見ると、以下のように考察できるかと思います。

SVDとNMFと同じタイトルがいくつか見られます("Clerks (1994)"や"One Flew Over the Cuckoo's Nest (1975)")
- ですが、SVDやNMFと比較すると、SF要素が弱く、納得感が低いように見えます(バイアスの影響が大きかったのかもしれません)
ユーザ同士で同じタイトルが推薦されています("Paths of Glory (1957)", "Clerks (1994)", Third Man, The (1949)など)
- 類似したユーザと捉えることはできている
267の方が全体的に予測した評価値が高くなっています
- ユーザのバイアスの影響を受けています(267の平均評価値が3.9に対して、868は3.0)

User ID: 267
42: Clerks (1994) [5.343020693286839]
516: Local Hero (1983) [5.306247713944661]
1449: Pather Panchali (1955) [5.267915793013931]
511: Lawrence of Arabia (1962) [5.217895974837784]
357: One Flew Over the Cuckoo's Nest (1975) [5.210585560183143]
960: Naked (1993) [5.165327044088528]
641: Paths of Glory (1957) [5.1401291180844675]
1512: World of Apu, The (Apur Sansar) (1959) [5.123277190111157]
513: Third Man, The (1949) [5.109739675120826]
652: Rosencrantz and Guildenstern Are Dead (1990) [5.06174853656031]

User ID: 868
641: Paths of Glory (1957) [6.020237492858888]
522: Down by Law (1986) [5.515328289793725]
171: Delicatessen (1991) [5.411841155332155]
513: Third Man, The (1949) [5.308531517941752]
42: Clerks (1994) [5.307793583401524]
262: In the Company of Men (1997) [5.251078640118084]
430: Duck Soup (1933) [5.223552176891947]
836: Ninotchka (1939) [5.205202414859825]
443: Birds, The (1963) [5.204741054839308]
519: Treasure of the Sierra Madre, The (1948) [5.189719602700117]

まとめ

欠測値やバイアスを考慮した行列分解(SVD)によるレコメンドを実装し、MovieLens100Kに適用しました。
また、確率的勾配降下法にミニバッチを導入することで、巨大な評価値行列を扱う実用ケースにおいても、なんとか耐えうる実装にしました。