Pythonで実装しながら緑本を学ぶ (第2章確率分布と統計モデルの最尤推定)

データ解析のための統計モデリング入門(通称、緑本)を読み始めました。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第2章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter2.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

2 確率分布と統計モデルの最尤推定

2.1 例題：種子数の統計モデリング

著者・久保氏のサポートサイトから提供されているデータ(架空の植物50個体の種子数)を使って、要約値(最大・最小、標本平均、四分位数など)を表示しています。

私の実装では、UCIで提供されているStudent Performance Data Setを使いました。
データの詳細は以下ですが、その中でもカウントデータとなっている数学の欠席数を説明変数として取り上げます(生徒数389人、欠席数30以上の生徒は除外しています)。

https://archive.ics.uci.edu/ml/datasets/student+performance

zipファイルはzipfileモジュールで簡単に解凍できます。

import zipfile


# カレントディレクトリに解凍
zfile = zipfile.ZipFile('student.zip')
zfile.extractall('.')

PandasのDataFrameにロードして欠席数(absences)をヒストグラムに描くと、以下のようになりました。
なぜか奇数の分布が少ないことがわかります。数学の授業は2時間連続となっており、1日休むと2回欠席したことになる(欠席数1の人は遅刻して2時間目の授業から出席した)などが考えられます。

f:id:ohke:20180117085651p:plain

そこで2で割って切り捨てることで、欠席数0〜1の人は0回、2〜3の人は1回、・・・となるように整形し、再度ヒストグラムを描きました。
以降では、この値を使うこととします。

f:id:ohke:20180117084948p:plain

2.2 データと確率分布の対応関係をながめる

データに見られるばらつきを表すために、確率分布を導入する。

確率分布とは、確率変数の値とそれが出現する確率を対応させたものです。
確率変数は、今回の例では、ある生徒iの欠席数 $y_i$ のことで、生徒毎にばらつきのある変数です。したがって、例えば「 $y_i=1$ の発生確率はいくらか」「 $y_i=2$ の発生確率はいくらか」・・を表現するものが確率分布です。

欠席数データのヒストグラムに、平均2.47のポアソン分布を重ねた図が、以下となります。
漸近的な減少傾向はポアソン分布で表せているようですが、当てはまりはそこまで良くないようです(「当てはまり」の定量的な評価は、この後行います)。

f:id:ohke:20180117142048p:plain

Pythonでポアソン分布の擬似乱数を生成するには、numpy.randomのpoissonメソッドを使う方法とscipy.stats.poissonのrvsメソッドを使う方法の、2つがあります。
以下のコードはいずれも平均2.47のポアソン分布に従う擬似乱数10,000個を生成しています。

import numpy as np
from scipy.stats import poisson


# 平均2.47のポアソン分布に従う擬似乱数10,000個を生成
poisson_values = np.random.poisson(lam=2.47, size=10000)
poisson_values = poisson.rvs(2.47, size=10000)

2.3 ポアソン分布とは何か？

ポアソン分布は以下の式で表現される確率分布です。

$p(y \mid \lambda)=\frac{\lambda^{y}exp(-\lambda)}{y!}$

パラメータはλのみ
$y \in {0, 1, 2, ..., ∞}$ の値を取り、全てのyの総和が1となる
確率分布の平均はλ(λ≧0)
分散と平均は等しい
観測データ同士は独立し、相関や相互作用は無いという前提も置いている

λ∈{3.5, 7.7, 15.1}の3パターンのポアソン分布を以下のようになります。

f:id:ohke:20180118080332p:plain

あるポアソン分布における確率分布を計算するためには、scipy.stats.poissonのpmfメソッドを使います。

# 平均3.5のポアソン分布で、確率変数が0〜14の時の確率分布を計算
prod = [poisson.pmf(i, 3.5) for i in range(15)]
# [0.030, 0.106, 0.185, 0.216, 0.189, 0.132, 0.077, 0.039, 0.017, 0.007, 0.002, 0.001, 0.000, 0.000, 0.000]

欠席数データへのポアソン分布の当てはまりが悪く感じられたのは、平均と分散が近くない(平均2.47に対して分散7.95)ためと思われます。

print('平均: {}'.format(data.mean())) # 平均: 2.47
print('分散: {}'.format(data.var())) # 分散: 7.95

2.4 ポアソン分布のパラメーターの最尤推定

確率分布のパラメータ(ポアソン分布の場合はλ)を、観測データに基いて推定することを最尤推定(法)という。

最尤推定法は、当てはまりの良さを表す尤度を最大化するパラメータを探す。
ポアソン分布の尤度L(λ)以下の式で求められます(要するに「 $y_1$ である」かつ「 $y_2$ である」かつ・・・でN個の事象が同時に起こる確率を求めてます)。

$L(\lambda) = p(y_1 \mid \lambda) \times p(y_2 \mid \lambda) \times \dots \times p(y_N \mid \lambda) = \prod_{i}^{N}p(y_i \mid \lambda) = \prod_{i}^{N}\frac{\lambda^{y_i}exp(-\lambda)}{y_{i}!}$

アンダーフローを防ぐために、対数変換した対数尤度関数が使われます。

$\log L(\lambda)=\sum_i^N (y_i \log \lambda - \lambda - \sum_k^{y_i} \log k)$

λを0.5〜3.0まで0.01刻みで変化させた時の、欠席数データに対する対数尤度関数の値をプロットしました。λ=2.5付近で最大となることがわかります。

f:id:ohke:20180118084906p:plain

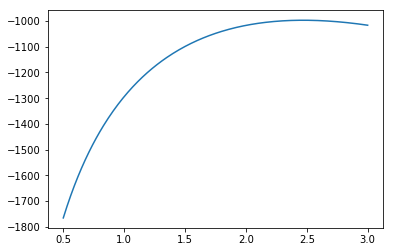
対数尤度関数が最大値となるλを最尤推定量といい、 $\hat{\lambda}$ とします。
$\hat{\lambda}$ は対数尤度関数の傾きが0となる点であるため、λで偏微分します。

$\frac{\partial L(\lambda)}{\partial\lambda}=\sum_i^N(\frac{y_i}{\lambda}-1)=\frac{1}{\lambda}\sum_i^{y_i}-N$

傾きが0の時、 $\hat{\lambda}$ は標本平均( $\frac{1}{N}\sum_i y_i$ )となります。

2.5 統計モデルの要点：乱数発生・推定・予測

モデルの良さは、そのモデルの予測の良さで決まる。

与えられた観測データがポアソン分布という仮定を置き、パラメータλを求めることが推定(あてはめ)と言う
推定で得られた統計モデルを使い、未知の観測データの分布を見積もることが予測

2.6 確率分布の選び方

確率分布は説明変数の性質に着目して選択する。

確率分布	離散 or 連続	範囲	標本分散と標本平均の関係
ポアソン分布	離散値	0以上(上限無し)	平均≒分散
二項分布	離散値	0以上で有限範囲	分散は平均の関数
正規分布	連続値	[-∞, +∞]	分散は平均と無関係
ガンマ分布	連続値	[0, +∞]	分散は平均の関数