2018-01-31

Pythonで実装しながら緑本を学ぶ (第4章 GLMのモデル選択)

Python 統計学読書メモ

前回から引き続き、データ解析のための統計モデリング入門(通称、緑本)を読み進めています。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第4章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter4.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

4 GLMのモデル選択 -AICとモデルの予測の良さ-

モデルが複雑になるほど、観測データに対する当てはまりは良くなってしまうため、「当てはまりの良いモデル=良いモデル」ではない。

「良い予測を行うモデル=良いモデル」という前提のもと、AICではこの「予測の良さ」を測る。

第3章で扱われている架空植物100個体の種子数のデータを使います。以下の著者サイトから入手できます。目的変数は種子数(y)です。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html

この投稿では種子数データと呼ぶことにします。

4.1 データはひとつ、モデルはたくさん

種子数を予測するモデルを検討する。

前章で現れた3つのモデルに、一定モデル( $\lambda=exp\beta_1$ )を加えた4つのモデルについて考える。

体サイズ( $x_i$ )が影響するxモデル(xモデル)
施肥処理( $f_i$ )が影響するyモデル(yモデル)
体サイズと施肥処理の両方が影響するx+fモデル
体サイズも施肥処理も影響しない一定モデル

xモデルで推定した結果は以下となります。第3章で得られたものと同じです。

results = sm.GLM(data['y'], sm.add_constant(data['x']), family=sm.families.Poisson()).fit()

f:id:ohke:20180129092531p:plain

4.2 統計モデルの当てはまりの悪さ：逸脱度

これまで、当てはまりの良さを対数尤度 $\log L$ で測ってきました。最も当てはまりの良いモデルは最大対数尤度として、 $\log L*$ とします。

$\log L(\lambda)=\sum_i(y_i\log\lambda-\lambda-\sum_k^{y_i}\log k)$

この最大対数尤度を使い、当てはまりの悪さを逸脱度Dとして定義する(-2をかけただけです)。

$D=-2\log L*$

ポアソン分布モデルで可能な最小逸脱度から、モデルの逸脱度Dを引いたものを、そのモデルの残差逸脱度とする。

ポアソン分布モデルで可能な最小逸脱度は、 $y_1=6$ なので $\lambda_1=6$ 、 $y_2=6$ なので $\lambda_2=6$ ・・・と全データを使ってあてはめた、つまり $\lambda_i=y_i$ となるモデルの逸脱度となります。この比較用の統計モデルは(Rでは)フルモデルと呼ばれます。フルモデルの逸脱度D*は以下で計算されます。

$D*=-2 \times \sum_i \log \frac{y_i^{y_i}exp(-\lambda)}{y_i!}$

フルモデルの最大対数尤度は-192.89、逸脱度は385.78となります。
xモデルの逸脱度は470.78(-2*-235.39)であることから、残差逸脱度は85.0(470.78-385.78)と計算されます(上の結果の"Deviance"と値が一致していることがわかります)。

# フルモデルの最大対数尤度
full_ll = sum([poisson.logpmf(y_i, y_i) for y_i in data['y']])

# フルモデルの逸脱度(最小逸脱度)
full_deviance = (-2) * full_ll

この残差逸脱度が最大になるモデル(=最もあてはまりの悪いモデル)もあります。切片 $\beta_1$ のみの一定モデルがこれに該当し、Rではnull modelと呼ばれます。
この時の残差逸脱度は89.5となります。

results = sm.GLM(data['y'], np.ones(len(data)), family=sm.families.Poisson()).fit()

f:id:ohke:20180129092805p:plain

4.3 モデル選択規準 AIC

「予測の良さ」を重視したモデルの選択規準としてAICを導入する。

最尤推定するパラメータの個数をkとするとAICは以下で計算されます。このAICが小さいモデルが良いモデルとなるため、最小のモデルを選択することになります。

$AIC=-2(\log L*-k)=D+2k$

残差逸脱度(あてはまりの悪さ)+パラメータ数×2なので、直感的には2kがモデルの複雑度に対するペナルティとなっているように見えます。

4.5 なぜAICでモデル選択してよいのか？

予測の良さを表す平均対数尤度を導入する。そして、最大対数尤度と平均対数尤度の差であるバイアスが、パラメータの数と一致することを示すことで、AICによって予測の良さを計測できることを説明する。

まずは真のモデルを知っている状態からスタートするために、 $\lambda=8$ のポアソン分布モデルから生成される50個のデータを生成します。

np.random.seed(10) # 一定の値になるようにシードを0で固定

# xに4〜12のポアソン乱数をセット
data_random = pd.DataFrame(np.random.poisson(8, 50), columns=['y'])

この時の平均値は7.44となっており、真のモデルから少し外れていることがわかります。

f:id:ohke:20180127140815p:plain

この50個のデータを観測されたデータとして、一定モデルでの最尤推定を行います。
切片2.0069( $\fallingdotseq exp(7.44)$ )で、その時の最大対数尤度は-116.47となります。

model = smf.poisson('y ~ 1', data=data_random)
results = model.fit()

f:id:ohke:20180127141128p:plain

最大対数尤度は、たまたま得られた観測データに対するあてはまりの良さでした。
予測の良さ、つまり他のデータにも適用できるかどうかを調べたいのですが、今回は真のモデルを知っているため、この真のモデルから新たにデータ(ここでは50データ×200セット)を作り出します。
そして上で得られたモデルを使って各セットの対数尤度を計算し、その平均値を求めます。これを平均対数尤度( $E(\log L)$ と表記)と呼びます。

平均対数尤度を計算すると-122.48となり、最大対数尤度と比較すると約6小さい(=あてはまりが悪い)ことがわかります。

# 真のモデルから200セットのデータを生成
data_random_200 = [pd.DataFrame(np.random.poisson(8, len(data_random)), columns=['y']) for i in range(200)]

# 200セットのデータに対して、β1=2.0069で200個の対数尤度を計算
lls = []
for d in data_random_200:
    lls.append(sum(poisson.logpmf(d, math.exp(results.params['Intercept']))))
    
# 平均対数尤度を計算
elogl = np.sum(lls) / len(lls)

「1セットで最大対数尤度を求め、そのモデルを使って200セットの平均対数尤度を求める」というのを200回繰り返してプロットした結果が、以下です。概ね、平均対数尤度(青▲)が最大対数尤度(赤●)よりもあてはまりが悪いことがわかります(ただし、常に平均対数尤度<最大対数尤度とも限らず、ばらつきは大きいものになってます)。
最大対数尤度と平均対数尤度の差をバイアスと呼びます。今回の例では、200回の平均バイアスは1.25となりました。

$b=\log L*-E(\log L)$

f:id:ohke:20180127143912p:plain

一般的に真のモデルは不明です。つまり $E(\log L)$ は未知の値となるはずです。
しかし、最尤推定するパラメータをk個持つモデルの平均対数尤度の推定量は、 log L-kとなることが、解析的かつ一般的に導出されている。これにより、先程導入したバイアスb=パラメータ数kと言えることにも着目してください。一定モデルはk=1のため、今回はE(log L)=log L-1となります。

AICはこれに-2をかけたもので、 $AIC=-2(\log L*-1)$ です。
平均対数尤度は予測の良さを表すので、AICの値が小さいほど、予測の良いモデルと言えます。

これまでは目的変数yだけのモデルを見てきました。これに説明変数xも導入して、2つのモデルを評価します。y、xのいずれも乱数で生成され、2つの変数の間に何の関係も無いデータとします(xは予測の役に立たない変数のはずです)。

$\log\lambda_i=\beta_1$ : 一定モデル(k=1)
$\log\lambda_i=\beta_1+\beta_2x_i$ : xモデル(k=2)

まずはデータ200セットで最大対数尤度を比較します。
以下のグラフは(xモデルの最大対数尤度 - 一定モデルの最大対数尤度)の分布ですが、xモデルの方が平均すると0.46大きくなっています。関係ないはずのxを使った何らかのあてはめの方が最大対数尤度は良くなることが確認できます。

f:id:ohke:20180128161734p:plain

一方で、平均対数尤度の差(xモデルの平均対数尤度 - 一定モデルの平均対数尤度)を比較すると、今度は逆に一定モデルの方が平均0.48大きくなります。

f:id:ohke:20180128162527p:plain

したがって、バイアスの差(最大対数尤度の差 - 平均対数尤度の差)は平均0.95で、パラメータ数の差(2-1=1)に近い値となっていることがわかります。分布でもそれほどばらつきが大きくなっていません。
今回の例のように、ネストしたモデル(xモデルが一定モデルの変数 $\beta_1$ も包含している)の場合、バイアスもばらつきが小さくなります。

f:id:ohke:20180128164353p:plain

200セットの内の1つ目のデータでAICを比較すると、一定モデル:258.1 < xモデル:259.0で、一定モデルを選択すべきとなります(逆に、説明変数xを追加したことで最大対数尤度が1以上増加した場合、xモデルを選択すべきと判定されます)。

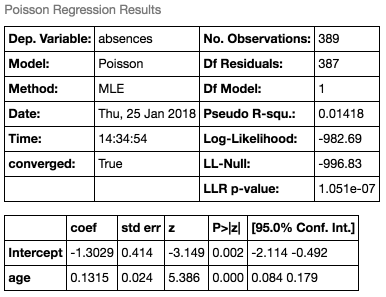
欠席数データに対してAICでモデルを選択する

最後に、以前の投稿でも使った欠席数のデータで、AICによるモデル選択を見ていきます。

このデータはUCIで提供されているStudent Performance Data Setです。目的変数は欠席数(absences)です(これまで同様、外れ値の除去や、欠席2回を1回とカウントするなど、若干の前処理を行っています)。
https://archive.ics.uci.edu/ml/datasets/student+performance

f:id:ohke:20180131140254p:plain

ここでは2つのモデルを比較します。

年齢(age)が欠席数に影響を与えるとするageモデル
どの変数も欠席数に影響を与えないとする一定モデル

# ageモデルを作る
age_model = smf.poisson('absences ~ age', data=student_data)

f:id:ohke:20180131140426p:plain

# 一定モデルを作る
const_model = smf.poisson('absences ~ 1', data=student_data)

f:id:ohke:20180131140446p:plain

一定モデルの最大対数尤度-996.8に対して、ageモデル-982.7で、約5.9改善されていることがわかります。

次に、フルモデルを求めます。最大対数尤度は-392.9(最小逸脱度は786.7)となります。

# フルモデルの最大対数尤度
full_model_ll = sum([poisson.logpmf(y_i, y_i) for y_i in student_data['absences']])
# -392.854706449

# フルモデルの逸脱度(最小逸脱度)
full_model_deviance = (-2) * full_model_ll
# 785.709412899

最後に、フルモデルとの残差逸脱度を計算します。

# 一定モデルの残差逸脱度
const_model_d = -2 * (const_model_results.llf - full_model_ll)
# 1207.95059528

# ageモデルの残差逸脱度
age_model_d = -2 * (age_model_results.llf - full_model_ll)
# 1179.67358728

AICはそれぞれ一定モデルで1210.0(=1208.0+2)、ageモデルで1183.7(=1179.7+4)となり、ageモデルを選択すべき、という結論になります。

2018-01-25

Pythonで実装しながら緑本を学ぶ (第3章一般化線形モデル(GLM))

Python 統計学読書メモ

データ解析のための統計モデリング入門(通称、緑本)を読み始めました。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。

今回は第3章です(前回の投稿はこちら)。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter3.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

3 一般化線形モデル(GLM)

個体ごとに異なる説明変数によって応答変数が変化する統計モデルとしてポアソン回帰を導入する。ポアソン回帰は一般線形化モデル(GLM)の一つです。

この章では2つのデータを使います。
1つは、第3章で扱われている架空植物100個体の種子数のデータで、著者サイトから入手できます。目的変数は種子数(y)です。
http://hosho.ees.hokudai.ac.jp/~kubo/ce/IwanamiBook.html
もう1つは、前回の投稿でも使いました、UCIで提供されているStudent Performance Data Setです。目的変数は欠席数(absences)です(前回同様、外れ値の除去や、欠席2回を1回とカウントするなど、若干の前処理を行っています)。
https://archive.ics.uci.edu/ml/datasets/student+performance

この投稿では種子数データ、欠席数データとそれぞれ呼ぶことにします。

3.1 例題: 個体ごとに平均種子数が異なる場合

種子数データでは、以下の個体差がある架空の植物100個体を想定している。個体差はいずれも観測データとして与えられている。平均種子数に影響を与えているのかについて知りたい。

体サイズ $x_i$
施肥処理の有無(50個体は施肥処理有り) $f_i$

f:id:ohke:20180125211542p:plain

また、欠席数データでは、以下の特徴(個体差)を持つ生徒389人に対して、欠席数(absences)との関係を調べます。

年齢 (age)
恋人がいるかどうか (romantic)

f:id:ohke:20180125211612p:plain

3.2 観測されたデータの概要を調べる

Pandasでデータの概要を見る場合は、head()で先頭5行、info()でデータの型、value_counts()で値の分布、describe()で要約統計量をそれぞれ出力すると良いかと思います。

# 先頭5行の表示
data.head()

# 各列の型
data.info()

# fの値の分布
data['f'].value_counts()

# 数値列(x列とy列)の要約統計量
data.describe()

3.3 統計モデリングの前にデータを図示する

散布図と箱ひげ図でデータの分布を視覚化します。

種子数データでは、散布図では体サイズが大きくなるほど種子数も増える傾向が見られますが、箱ひげ図からは施肥処理による種子数の変化は読み取れません。

# 散布図
plt.scatter(data[data['f']=='C']['x'], data[data['f']=='C']['y'], marker='o', label='C')
plt.scatter(data[data['f']=='T']['x'], data[data['f']=='T']['y'], marker='x', label='T')
plt.legend(loc='best')
plt.show()

f:id:ohke:20180124092516p:plain

# 箱ひげ図
fig, ax = plt.subplots()
ax.boxplot([data[data['f']=='C']['y'], data[data['f']=='T']['y']])
ax.set_xticklabels(['C', 'T'])
plt.show()

f:id:ohke:20180124092533p:plain

次に欠席数データについて見てみます。

散布図では、17歳をピークとした山になっていますが、概ね年齢が上がると欠席数も増える傾向がありそうです。箱ひげ図では、恋人がいる方が欠席数は多くなることが伺えます。

f:id:ohke:20180125142237p:plain

f:id:ohke:20180125142247p:plain

3.4 ポアソン回帰の統計モデル

個体iの種子数 $y_i$ がポアソン分布に従っていると仮定します。

$p(y_i\mid\lambda_i)=\frac{\lambda_i^{y_i}exp(-\lambda_i)}{y_i !}$

個体ごとに異なる平均 $\lambda_i$ を説明変数(共変量) $x_i$ の関数として、仮に以下で定義する。 $\beta_i$ はパラメータ(係数)と呼び、当てはまりの良い値を選ぶ。

$\lambda_i=\beta_i+\beta_2 x_i \Leftrightarrow \log\lambda_i=\beta_1+\beta_2 x_i$

右辺 $\beta_1+\beta_2 x_i$ は、線形予測子
左辺の関数は、リンク関数
- 対数( $\log\lambda_i$ )の場合は、対数リンク関数と呼ばれ、ポアソン分布に使われる
- 対数リンク関数、ロジットリンク関数(ロジスティック回帰で用いる)は、正準リンク関数と呼ばれる

当てはまりの良さは対数尤度関数で定量化し、対数尤度が最大となる $\hat{\lambda_i}$ を求めていましたが、それを今回導入したパラメータの関数に置き換えます。以下の関数を最大にする ${\beta_1, \beta_2}$ を求めます。

$\log L(\beta_1,\beta_2)=\sum_i\log\frac{\lambda_i^{y_i}exp(-\lambda_i}{y_i !}$

最尤推定量は、Rだと> fit <- glm(y ~ x, data = d, family = poisson)で求められますが、PythonではstatsmodelやPyStanでこうした計算が簡単に行なえます。今回はstatsmodelを使います。

http://www.statsmodels.org/stable/index.html

以下のコードではいずれも最尤推定を計算しています。実行前にstatsmodelsをインストール( pip install statsmodels )する必要があります。
statsmodelsには2種類のAPI(statsmodels.apiとstatsmodels.formula.api)があります。statsmodels.apiでは説明変数と目的変数を受け取るピュアな関数が提供されます。一方、statsmodels.formula.apiでは目的変数と説明変数の関係式をRのフォーマットで渡せます。

import statsmodels.api as sm

# 最尤推定(切片も含む場合はadd_constant()で値を渡す)
results = sm.Poisson(data['y'], sm.add_constant(data['x'])).fit()
#results = sm.GLM(data['y'], sm.add_constant(data['x']), family=sm.families.Poisson()).fit()
# 結果の出力
results.summary()

import statsmodels.formula.api as smf

# 最尤推定
results = smf.poisson('y ~ x', data=data).fit()
# 結果の出力
results.summary()

結果は以下のように出力されます。

最尤推定値(coef)はそれぞれ、 (Interceptまたはconst)は1.2917、 (x)は0.0757
- 標準誤差(std err)は、最尤推定値のばらつき
- z値(z value)は、最尤推定値÷標準誤差で、推定値が0から十分離れていることの目安
- Pr|>z|は、マイナス無限大から0までの値をとる確率
このときの最大対数尤度(Log-Likelihood)は-235.39

f:id:ohke:20180120160400p:plain

同様に、欠席数データに対しても適用すると、以下の結果になります。
最尤推定値(coef)は、 $\hat{\beta_1}$ (Intercept)は-1.3029、 $\hat{\beta_2}$ (age)は0.1315で、このときの最大対数尤度は-982.69です。第2章のモデルの最大対数尤度は-996.83( $\lambda=2.47$ の時)だったので、それよりも当てはまりの良いモデルとなっていることがわかります(ちなみに $\lambda$ が一定のモデルの最大対数尤度はLL-Nullの値と一致します。第4章で詳しく見ていきます)。

f:id:ohke:20180125195640p:plain

3.5 説明変数が因子型の統計モデル

施肥処理の有無を表す $f_i$ のように、Rでは数量型以外で特定の値(水準)をとる変数を因子型と言います。因子型の場合は、ダミー変数に置き換えてモデル化します。

施肥処理の効果のみを考慮した以下のモデルでは、 $d_i$ がダミー変数ですが、 $f_i=C$ の時は $d_i=0$ 、 $f_i=T$ の時は $d_i=1$ となるようにします。

$\lambda_i=exp(\beta_1+\beta_3 d_i)$

pandasではget_dummies()でダミー変数に置き換えることができます。

# f=Tの場合に1となる列d(ダミー変数)を追加
data['d'] = pd.get_dummies(data['f'])['T']

結果は以下のとおりです。
0か1しか値を持たないにもかかわらず、最尤推定値は0.0128と小さな値となっていることから、種子数に対する影響は小さいことがわかります。

f:id:ohke:20180125195640p:plain

欠席数データに対しても、恋人の有無をダミー変数に置き換えたモデルを作りました。
こちらは、最尤推定値が0.2250でそれなりに影響力はありそうです。

f:id:ohke:20180125200930p:plain

3.6 説明変数が数量型＋因子型の統計モデル

複数の説明変数を組み合わせる場合は、線形予測子で和として表現する。

$\log\lambda_i=\beta_1+\beta_2 x_i+\beta_3 d_i$

Pythonでも単純で、'y ~ x+d'と表現できます。

results = smf.poisson('y ~ x+d', data=data).fit()

種子数データの結果を見ると、fはマイナスの推定値となっており、種子数については逆効果となりそうです。一方、最大対数尤度は少し良くなっています。

f:id:ohke:20180125205112p:plain

得られた最尤推定値を当てはめると、 $\lambda_i$ は以下の式で導出されます。logが取り払われたことで、乗算で $\lambda_i$ に影響を与えることがわかります。

$\lambda_i=exp(1.26+0.08x_i-0.032d_i)$

欠席数データでは、 $\lambda_i$ は以下の式になります。2変数となったことで、最大対数尤度も-979.35と良くなっています。

$\lambda_i=exp(-1.2045+0.1219\times age_i+0.1752d_i$

f:id:ohke:20180125205326p:plain

3.7 「何でも正規分布」「何でも直線」には無理がある

確率分布を等分散の正規分布、リンク関数を恒等リンク関数(何もしない、つまり $\lambda_i=\beta_1+\beta_2 x_i+\beta_3 d_i$ で表現される $\lambda_i$ )にすると、線形モデル(LM)と呼ばれる。

そのLMの1つが直線回帰です。直線回帰は以下の特徴を持つため、今回のカウントデータでは不適切といえる。

応答変数Yは平均で標準偏差ρの正規分布に従うと仮定
- 正規分布では連続値を扱う
- ばらつきも一定
平均値は
- 負の値をとり得る

応答変数にあわせて、確率分布は適切に選ぶべき。

2018-01-19

Pythonで実装しながら緑本を学ぶ (第2章確率分布と統計モデルの最尤推定)

Python 統計学

今回は第2章です。実装は以下で公開しています。

introduction_to_machine_learning_with_python/chapter2.ipynb at master · ohke/introduction_to_machine_learning_with_python · GitHub

2 確率分布と統計モデルの最尤推定

2.1 例題：種子数の統計モデリング

著者・久保氏のサポートサイトから提供されているデータ(架空の植物50個体の種子数)を使って、要約値(最大・最小、標本平均、四分位数など)を表示しています。

私の実装では、UCIで提供されているStudent Performance Data Setを使いました。
データの詳細は以下ですが、その中でもカウントデータとなっている数学の欠席数を説明変数として取り上げます(生徒数389人、欠席数30以上の生徒は除外しています)。

https://archive.ics.uci.edu/ml/datasets/student+performance

zipファイルはzipfileモジュールで簡単に解凍できます。

import zipfile


# カレントディレクトリに解凍
zfile = zipfile.ZipFile('student.zip')
zfile.extractall('.')

PandasのDataFrameにロードして欠席数(absences)をヒストグラムに描くと、以下のようになりました。
なぜか奇数の分布が少ないことがわかります。数学の授業は2時間連続となっており、1日休むと2回欠席したことになる(欠席数1の人は遅刻して2時間目の授業から出席した)などが考えられます。

f:id:ohke:20180117085651p:plain

そこで2で割って切り捨てることで、欠席数0〜1の人は0回、2〜3の人は1回、・・・となるように整形し、再度ヒストグラムを描きました。
以降では、この値を使うこととします。

f:id:ohke:20180117084948p:plain

2.2 データと確率分布の対応関係をながめる

データに見られるばらつきを表すために、確率分布を導入する。

確率分布とは、確率変数の値とそれが出現する確率を対応させたものです。
確率変数は、今回の例では、ある生徒iの欠席数 $y_i$ のことで、生徒毎にばらつきのある変数です。したがって、例えば「 $y_i=1$ の発生確率はいくらか」「 $y_i=2$ の発生確率はいくらか」・・を表現するものが確率分布です。

欠席数データのヒストグラムに、平均2.47のポアソン分布を重ねた図が、以下となります。
漸近的な減少傾向はポアソン分布で表せているようですが、当てはまりはそこまで良くないようです(「当てはまり」の定量的な評価は、この後行います)。

f:id:ohke:20180117142048p:plain

Pythonでポアソン分布の擬似乱数を生成するには、numpy.randomのpoissonメソッドを使う方法とscipy.stats.poissonのrvsメソッドを使う方法の、2つがあります。
以下のコードはいずれも平均2.47のポアソン分布に従う擬似乱数10,000個を生成しています。

import numpy as np
from scipy.stats import poisson


# 平均2.47のポアソン分布に従う擬似乱数10,000個を生成
poisson_values = np.random.poisson(lam=2.47, size=10000)
poisson_values = poisson.rvs(2.47, size=10000)

2.3 ポアソン分布とは何か？

ポアソン分布は以下の式で表現される確率分布です。

$p(y \mid \lambda)=\frac{\lambda^{y}exp(-\lambda)}{y!}$

パラメータはλのみ
$y \in {0, 1, 2, ..., ∞}$ の値を取り、全てのyの総和が1となる
確率分布の平均はλ(λ≧0)
分散と平均は等しい
観測データ同士は独立し、相関や相互作用は無いという前提も置いている

λ∈{3.5, 7.7, 15.1}の3パターンのポアソン分布を以下のようになります。

f:id:ohke:20180118080332p:plain

あるポアソン分布における確率分布を計算するためには、scipy.stats.poissonのpmfメソッドを使います。

# 平均3.5のポアソン分布で、確率変数が0〜14の時の確率分布を計算
prod = [poisson.pmf(i, 3.5) for i in range(15)]
# [0.030, 0.106, 0.185, 0.216, 0.189, 0.132, 0.077, 0.039, 0.017, 0.007, 0.002, 0.001, 0.000, 0.000, 0.000]

欠席数データへのポアソン分布の当てはまりが悪く感じられたのは、平均と分散が近くない(平均2.47に対して分散7.95)ためと思われます。

print('平均: {}'.format(data.mean())) # 平均: 2.47
print('分散: {}'.format(data.var())) # 分散: 7.95

2.4 ポアソン分布のパラメーターの最尤推定

確率分布のパラメータ(ポアソン分布の場合はλ)を、観測データに基いて推定することを最尤推定(法)という。

最尤推定法は、当てはまりの良さを表す尤度を最大化するパラメータを探す。
ポアソン分布の尤度L(λ)以下の式で求められます(要するに「 $y_1$ である」かつ「 $y_2$ である」かつ・・・でN個の事象が同時に起こる確率を求めてます)。

$L(\lambda) = p(y_1 \mid \lambda) \times p(y_2 \mid \lambda) \times \dots \times p(y_N \mid \lambda) = \prod_{i}^{N}p(y_i \mid \lambda) = \prod_{i}^{N}\frac{\lambda^{y_i}exp(-\lambda)}{y_{i}!}$

アンダーフローを防ぐために、対数変換した対数尤度関数が使われます。

$\log L(\lambda)=\sum_i^N (y_i \log \lambda - \lambda - \sum_k^{y_i} \log k)$

λを0.5〜3.0まで0.01刻みで変化させた時の、欠席数データに対する対数尤度関数の値をプロットしました。λ=2.5付近で最大となることがわかります。

f:id:ohke:20180118084906p:plain

対数尤度関数が最大値となるλを最尤推定量といい、 $\hat{\lambda}$ とします。
$\hat{\lambda}$ は対数尤度関数の傾きが0となる点であるため、λで偏微分します。

$\frac{\partial L(\lambda)}{\partial\lambda}=\sum_i^N(\frac{y_i}{\lambda}-1)=\frac{1}{\lambda}\sum_i^{y_i}-N$

傾きが0の時、 $\hat{\lambda}$ は標本平均( $\frac{1}{N}\sum_i y_i$ )となります。

2.5 統計モデルの要点：乱数発生・推定・予測

モデルの良さは、そのモデルの予測の良さで決まる。

与えられた観測データがポアソン分布という仮定を置き、パラメータλを求めることが推定(あてはめ)と言う
推定で得られた統計モデルを使い、未知の観測データの分布を見積もることが予測

2.6 確率分布の選び方

確率分布は説明変数の性質に着目して選択する。

確率分布	離散 or 連続	範囲	標本分散と標本平均の関係
ポアソン分布	離散値	0以上(上限無し)	平均≒分散
二項分布	離散値	0以上で有限範囲	分散は平均の関数
正規分布	連続値	[-∞, +∞]	分散は平均と無関係
ガンマ分布	連続値	[0, +∞]	分散は平均の関数