データ解析のための統計モデリング入門(通称、緑本)を読み進めています。
述べられている理論を整理しつつ、Rでの実装をPythonに置き換えた際のポイントなども深掘りしていきます。
今回は第6章です。実装は以下で公開しています。
6 GLMの応用範囲を広げる -ロジスティック回帰など-
6.1 さまざまな種類のデータで応用できるGLM
第5章までは、ポアソン分布・対数リンク関数のGLMを扱ってきましたが、確率分布・リンク関数・線形予測子を組み替えることで様々なデータを表現できるようになる。
以下の表は、よく使われる確率分布とリンク関数の組み合わせです。なお、乱数生成はscipy.stats、familyとlinkの指定はstatsmodelsを使った場合の指定方法です。
| 確率分布 | 乱数生成 | family指定 | リンク関数 | link指定 | |
|---|---|---|---|---|---|
| 離散 | 二項分布 | binom | Binomial() | ロジット | logit |
| 離散 | ポアソン分布 | poisson | Poisson() | ログ | log |
| 離散 | 負の二項分布 | nbinom | NegativeBinomial() | ログ | log |
| 連続 | ガンマ分布 | gamma() | Gamma() | ログ? | log |
| 連続 | 正規分布 | norm() | Gaussian() | 恒等リンク | identity |
例えば、平均2・分散1の正規分布の乱数を5つ生成する場合は、以下のようになります。他の確率分布でもrvs()メソッドを使うことで生成できます
import scipy scipy.stats.norm(2, 1).rvs(5) # array([ 2.976, 0.886, 2.72 , 1.38 , 0.664])
ガウス分布・ログリンク関数のモデルを作る場合は、以下のように指定します。statsmodels.formula.api.familiesに確率分布、statsmodels.formula.api.linksにリンク関数用のPython関数がそれぞれ定義されています。
import statsmodels.formula.api as smf model = smf.glm(formula='y ~ x', data=data, family=sm.families.Gamma(link=sm.families.links.log))
6.2 例題:上限のあるカウントデータ
二項分布は上限の有るカウントデータ(応答変数が )となる現象のばらつきを表現するために使う。「同じ条件のN個の内、y個は陽性、N-y個は陰性」という構造のデータの説明に適している。
架空植物100個体のそれぞれが持つ 個(全て8に固定)の種子を観察し、発芽能力がある生きた種子は
個、死んだ種子は
個というデータが得られたとします。体サイズや施肥処理によって、生存確率に与える変化を調べます。
- 個体iの種子の生存確率を
とする
- 個体の大きさ
と施肥処理の有無
("T"ならば有り、"C"ならば無し)が
に影響を与えるとする
説明変数( と
)と応答変数(
)の分布を見てみると、体サイズが大きくなるほど、また、施肥処理すると生存種子数が増えることが伺えます。

6.3 二項分布で表現する「あり・なし」カウントデータ
「N個の内、y個」という構造のカウントデータを表現する統計モデルに二項分布がよく使われる。
二項分布の確率分布は以下で定義されます。 はN個中y個の事象が起きる確率です。
$$ p(y \mid N,q)={}_n \mathrm{C} _r q^y (1-q)^{N-y} $$
二項分布でq={0.1, 0.3, 0.5, 0.8}の時の確率pをプロットします。全てのyにおけるpの総和を計算すると、1となることにも注目です。

Pythonではscipy.stats.binomで二項分布の確率分布を計算できます。
from scipy.stats import binom # N=8, q=0.1の時に、y=1となる確率 p = binom.pmf(1, 8, 0.1)
6.4 ロジスティック回帰とロジットリンク関数
確率分布に二項分布、リンク関数にロジットリンク関数を指定したGLMが、ロジスティック回帰です。
二項分布では、事象が起きる確率(ここでは生存確率) を指定する必要があります。
の値の範囲
を表現するために適したリンク関数が、ロジットリンク関数です。
ロジットリンク関数は、ロジスティック関数の逆関数です。
ロジスティック関数は、以下の式で表現されます。 は線形予測子
です。
$$ q_i=logistic(z_i)=\frac{1}{1+\exp(-z_i)} $$
zを-6〜6で変化させた時に、qは以下のような曲線(シグモイドカーブ)を描きます。zがどのような値になっても に収まっていて都合が良いこと、またz=0でq=0.5となることに着目してください。

における、
のとき(左図)と、
のとき(右図)のシグモイドカーブをそれぞれ描いてみます。
においては右肩下がりになっており、負の傾きも表現できていることが確認できます。


ロジスティック関数を変形したときの、
$$ \log \frac{q_i}{1-q_i}=z_i $$
左辺がロジット関数となります。
$$ logit(q_i) = \log \frac{q_i}{1-q_i} $$
それではロジスティック回帰によるパラメータの推定を行います。
尤度関数と対数尤度関数は以下で定義され、 を最大にする推定値
を探し出します。
$$ L({\beta_j})=\prod_i {}_n \mathrm{C} _r q_i^{y_i}(1-q_i)^{N_i-y_i} $$
$$ \log L({\beta_j})=\sum_i {\log {}_n \mathrm{C} _r+y_i\log(q_i)+(N_i-y_i)\log(1-q_i)} $$
Rでは以下のように記述します。応答変数は(生存した数, 死んだ数)の2列100行で表現するため、cbindでその組み合わせを生成しています。
> glm(cbind(y, N-y) ~ x + f, data = data, family = binomial)
Pythonでは、statsmodelsで以下のように記述すると、同じ計算を行えます。cbindではなくI(N-y)となっている点に注意してください。
statsmodels.formula.apiのformulaで渡される式の解析にはpatsyが使われています。patsyにはcbindと同等の組み合わせを作るI()が定義されており、y+I(N-y)としています。
http://patsy.readthedocs.io/en/latest/index.html
import statsmodels.formula.api as smf results = smf.glm(formula='y + I(N - y) ~ x + f', data=data, family=sm.families.Binomial()).fit(disp=0)
結果を出力すると、 の時に最大対数尤度-133.11(残差123.03)が得られていることがわかります。

ロジット関数の線形予測子を得られた値で置き換えると、以下の式になります。
左辺は(生存する確率)/(生存しない確率)のオッズになっており、例えばxが1増加するとオッズは 倍になります。
$$ \frac{q_i}{1-q_i}=\exp(\beta_1+\beta_2 x_i+\beta_3 f_i)=\exp(\beta_1)+\exp(\beta_2 x_i)+\exp(\beta_3 f_i)=\exp(-19.54)+\exp(1.95x_i)+\exp(2.02f_i) $$
最後に、以下の4つのモデルからAICによる選択を行います。AICについては第4章の投稿も参考にしてください。
- 一定モデル(定数)
- xモデル
- fモデル
- x+fモデル
Rであれば、MASS packageのstepAICという関数を使えば、ネストしたモデルからAICで適切にパラメータを選択されるようです。
Pythonでは準じたものが無さそうなので、1つずつ線形予測子を定義してAICを計算しました。x+fモデルが272で最小となったため、このモデルを選択すべきとなります。
formulas = [
'y + I(N - y) ~ 1',
'y + I(N - y) ~ x',
'y + I(N - y) ~ f',
'y + I(N - y) ~ x + f'
]
results = []
for formula in formulas:
results.append(smf.glm(formula=formula, data=data, family=sm.families.Binomial()).fit(disp=0))
for i in range(4):
print(formulas[i], ':', results[i].aic)
# y + I(N - y) ~ 1 : 644.409341662
# y + I(N - y) ~ x : 364.345443284
# y + I(N - y) ~ f : 637.759753457
# y + I(N - y) ~ x + f : 272.211129285
6.5 交互作用項の入った線形予測子
交互作用項を追加した線形予測子を新たに導入します。
交互作用項は説明変数間の積で、観測データの複雑なパターンの抽出を狙ったものです。
Pythonでも、xとfの交互作用であればx:fで表現できます。
result = smf.glm(formula='y + I(N - y) ~ x + f + x:f', data=data, family=sm.families.Binomial()).fit()
最尤推定の結果、 となっています。fの係数
が-0.06とほとんど0に近づいてしまっており(交互作用項無しの場合は2.02)、
から
へ重みが移っています。
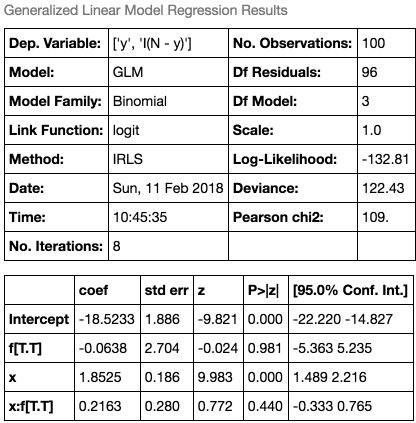
交互作用項無し(左図)と有り(右図)でそれぞれ予測値をプロットしてみると、モデル全体への変化は見られないことがわかります。AICで比較しても、交互作用項無しで272.2だったのに対して、有りで273.6と悪くなっています。


上で見たように、交互作用項を過大推定されることで、交互作用項を多数含んだ統計モデルはAICが最良になることがよくある。説明変数では説明できない(不足している)データでは特にその傾向が強いため、むやみに交互作用項を入れるのは避けるべき。
Red wine quality data setを使ったロジスティック回帰と交互作用項
UCIで提供されているRed wine quality data setに対して、ロジスティック回帰と交互作用項を適用してみます。
https://archive.ics.uci.edu/ml/datasets/Wine+Quality
このデータセットは、1599レコードからなります。各レコード0〜10(実際にデータがあるのは3〜8)の評価値と、アルコール度数やpH値などの情報11項目の値を持ちます。今回は、酢酸含有量(va)とアルコール度数(a)を説明変数、評価値(q)を応答変数とするモデルを作ります。

酢酸含有量およびアルコール度数と評価値の関係をプロットします。酢酸含有量と評価値には負の相関(左図)、アルコール度数と評価値には正の相関(右図)があることがわかります。


ロジスティック回帰
確率分布を二項分布、線形予測子を とした、リンク関数をロジット関数に設定したロジスティック回帰を行う。
result = smf.glm(formula='q + I(N - q) ~ va + a', data=data, family=sm.families.Binomial()).fit()
で、AIC=4719のモデルが得られました。

交互作用項
線形予測子に交互作用項を追加した において、ロジスティック回帰を行う。
result = smf.glm(formula='q + I(N - q) ~ va + a + va:a', data=data, family=sm.families.Binomial()).fit()
結果としては、例題同様、vaの係数 が多項式の係数
へ移る形となり、モデルを複雑にするだけの結果となりました(AICも4721で、交互作用項を含むことで予測精度は落ちていると判定できます)。

6.6 割算値の統計モデリングはやめよう
観測値の割算による統計モデリングは、2つの不具合を含む。ロジスティック回帰では「N個の内y個で事象が起きる確率」を明示的に扱うことで、割算値の使用を回避する。
- 割算値にすることで、情報が失われる (3/10と300/1000は確からしさは異なる)
- 誤差が入った数量同士の割算値は、確率分布が複雑になる (分子と分母が独立でない場合、さらにややこしい)
単位面積や単位時間あたりの数量を扱う上で便利なのがオフセット項です。
「観測地iにおける植物個体の密度が明るさ に与える影響を知る」というタスクを考えます。
- 100箇所で調査
- 観測地iの明るさ
と、植物個体数
を計測
- ただし、観測地毎の面積
は異なる
平均個体数 は面積×個体密度で求められます。このうち、個体密度は
に依存しているため、以下の式で表現できます。これは、線形予測子
・対数リンク関数・ポアソン分布のGLMです(もちろん割算無しです)。
$$ \lambda_i=A_i \times \mbox{個体密度}=A_i \exp(\beta_1+\beta_2x_i)=\exp(\beta_1+\beta_2 x_i+\log A_i) $$
には係数がついていない定数で、オフセット項と呼ばれます。
statsmodelsでも、GLMにoffsetオプションが提供されており、以下のように指定します。
result = smf.glm(formula='y ~ x', offset=np.log(data['A']), data=data, family=sm.families.Poisson()).fit()
6.7 正規分布とその尤度
正規分布(ガウス分布)は、連続値のデータを統計モデルで扱うための確率分布です。平均値 と、標準偏差
を指定します。確率密度関数
は以下のとおりです。
3パターンの確率密度関数を図示します。

ポアソン分布のように「x回発生する確率」といった離散確率分布と異なり、連続確率分布は「x1からx2までに収まる確率」といった範囲に入る確率の表現となります。例えば、 の正規分布において、yが1.2〜1.8となる確率
は、 積分の形で
となります。
Pythonでは、累積分布関数cdfで計算できます。
norm.cdf(1.8, 0, 1) - norm.cdf(1.2, 0, 1) # 0.079
正規分布の最尤推定では、尤度を確率密度の積で計算します。対数尤度関数は以下になります。 が0に近い場合、AICや逸脱度が負の値になることもあります。
$$ \log L(\mu,\sigma)=-0.5N\log (2\pi\sigma^2)-\frac{1}{2\sigma^2}\sum_i(y_i-\mu)^2 $$
対数尤度関数を見ると、 を最小となる
において
が最大となり、最小二乗法による推定と同等であることがわかります。
6.8 ガンマ分布のGLM
ガンマ分布は、取りうる確率変数が0以上の連続確率分布で、確率密度関数は以下です。平均は 、分散は
となります(sはshape、rはrateパラメータと呼ばれます)。
3パターンの確率密度関数を図示します。

Pythonで確率密度関数は以下のように計算できます。scaleは です。
from scipy.stats import gamma gamma.pdf(1, a=1, scale=1/1) # 0.368
Boston housing data setを使った正規分布とガンマ分布のGLM
scikit-learn付属のBoston housing data setを使い、正規分布とガンマ分布でGLMを行います。
https://www.cs.toronto.edu/~delve/data/boston/bostonDetail.html
このデータセットは、506レコードからなります。住宅価格の中央値と、犯罪発生率や平均部屋数などの13項目の値を持ちます。今回は、平均部屋数(RM)と低所得者の割合(LSTAT)を説明変数、住宅価格の中央値(y)を応答変数とするモデルを作ります。

正規分布
目的変数yが連続値ですが、0以上の値のため、正規分布ではあてはまりが良くなさそうですが、線形予測子 、恒等リンク関数として最尤推定を行います。
result = smf.glm(formula='y ~ RM', data=data, family=sm.families.Gaussian()).fit()
予測値をプロットすると以下のようになります。マイナスの予測値を含むこと(左下端)、恒等リンク関数のため直線回帰となっていることが確認できます。

さらに、LSTATを線形予測子に追加してみます。
result = smf.glm(formula='y ~ RM+LSTAT', data=data, family=sm.families.Gaussian()).fit()
実測値と予測値をプロットしました。またLSTAT={5, 15, 25, 35}の場合の予測値も直線で重ねています。LSTATが高くなるほど、直線が下に来ていることがわかります。

ガンマ分布
確率分布はガンマ分布、線形予測子は 、リンク関数にはlog関数を使って、最尤推定を行います。応答変数は0以上のため、正規分布よりも適切そうです。
result = smf.glm(formula='y ~ RM', data=data, family=sm.families.Gamma(link=sm.families.links.log)).fit()

リンク関数にlogを指定しているため、右肩上がりの曲線で予測されていることがわかります。














