論文メモ: Item2Vec: Neural Item Embedding for Collaborative Filtering

word2vecをリコメンデーションに応用した論文"Item2Vec: Neural Item Embedding for Collaborative Filtering"を読みましたので、そのメモとなります。

[1603.04259] Item2Vec: Neural Item Embedding for Collaborative Filtering

1. INTRODUCTION AND RELATED WORK

SGNS(skip-gram negative sampling, word2vec)をアイテムベースの協調フィルタリングに応用する。

それをitem2vecと名付け、SVDと比較して優位性を示す。

2. SKIP-GRAM WITH NEGATIVE SAMPLING

SGNSについて概観する(初出はこちらの論文)。

前処理まで完了した文章(単語列の形式で、例えばI have a pen.なら[I, have, a, pen])を ${(w_i)^K_{i-1}}$ 、文章内で現れる全単語を ${W={w_i}^W_{i=1}}$ とすると、skip-gramは以下の目的関数の最大化を目指して、確率的勾配降下法で学習する。

$\frac{1}{K} \sum^K_{i=1} \sum_{-c \le j \le c, j \ne 0} \log p(w_{i+j} \mid w_i)$

cはウィンドウサイズで、前後c単語(周辺単語と呼ぶ)を考慮する。
${p(w_j | w_i)}$ は、対象の単語 ${w_i}$ と周辺単語 ${w_{i+j}}$ の共起確率を表すソフトマックス関数です。

$p(w_j \mid w_i) = \frac{\exp(u^T_i v_j)}{\sum_{k \in I_W} \exp(u^T_i v_k)}$

${u_i}$ は対象単語のベクトル、 ${v_j}$ は周辺単語のベクトル、 ${I_W}$ は全単語のインデックスを表す。単語ベクトル長(mとする)はハイパーパラメータとして設定する。

上の式では、分母で全単語との総和を計算しているため、pの計算量は出現する全ての単語数(10⁵〜10⁶)に比例して増大してしまう。

negative samplingでは、周辺外単語の計算(分母の計算)は全ての単語について計算するのではなく、ランダムにサンプリングされたN個の単語についてのみ行うことで近似する。
以下の式になる。ただし、 ${\sigma(x) = 1/(1+\exp(-x))}$ と置いている。

$p(w_j \mid w_i) = \sigma(u^T_i v_j) \prod^N_{k=1} \sigma(-u^T_i v_k)$

なお、単語の出現頻度による偏りを防ぐために、出現頻度が高い単語はサンプリングされにくいように工夫する。
単語wの出現頻度をf(w)、閾値をρとすると、以下の確率で単語wはサンプリングから外す。

$p(discard \mid w)=1-\sqrt{\frac{\rho}{f(w)}}$

参考

SGNSについては、こちらの方の記事がとても参考になります。あわせて読むと理解が捗ります。

word2vecのソースを読んでみた - Qiita

Word2Vec のニューラルネットワーク学習過程を理解する · けんごのお屋敷

3. ITEM2VEC - SGNS FOR ITEM SIMILARITY

SGNSをアイテムベース協調フィルタリングへ組み込む方法について説明する。

SGNSでは単語列からある単語とその周辺の単語から関連性を計算していた。
アイテムベースCFでは、単語をアイテム、単語列をアイテム集合(バスケット)と置き換えることでSGNSを適用する。

列から集合となったことで、SGNSでは持っていた時間・位置の近接情報については、捨てることにした。
したがって目的関数からは、ウィンドウサイズを取り払い、以下の式に変更する。

$\frac{1}{K} \sum^K_{i=1} \sum^K_{j \ne i} log p(w_{i+j} \mid w_i)$

アイテムiのベクトルを ${u_i}$ とする。アイテム間の関連度はコサイン類似度で計算する。

以降では、このプロセスやこのプロセスで得られたアイテムベクトルを総称してitem2vecと呼ぶ。

4. EXPERIMENTAL SETUP AND RESULTS

SVDを比較対象とし、データセットを使った実験と評価を行う。

SVDは以下の手順でベクトルを作る。 item2vec同様、アイテム間のコサイン類似度を計算する。

K×Kの正方行列を用意する(Kはアイテム数)
- (i, j)の要素は ${(w_i, w_j)}$ の同時出現頻度が正規化された値がセットされる
正方行列を特異値分解して、行の単語ベクトルを得る
- Sは対角行列(K×K)で、Sから重要度の高いベクトルをm個を持つ(したがって、m次元まで圧縮できる)
- Uは左特異行列(K×K)
(SVDについて正しく理解できていないので、記述が誤っているかもしれません。)

評価には2種類のデータセットを使う。

Microsoft Xbox Musicの再生ログ
- 732,000ユーザと49,000アーティストの9,000,000再生ログ
Microsoft Storeの購入ログ
- 1,706アイテム、379,000オーダー
- 「同時に購入された」という情報のみを持つ(その他のユーザの情報は使わない)

まずはMusicデータセットについて、それぞれの手法(item2vecとSVD)でジャンル分けして、精度を見る。
t-SNEで2次元に可視化した結果が下の図(原文Fig.2を引用。左がitem2vec、右がSVD)で、概ねitem2vecの方がきれいに分離していることがわかる。(SVDは図右下で混在が見られる)。

f:id:ohke:20171130142811p:plain

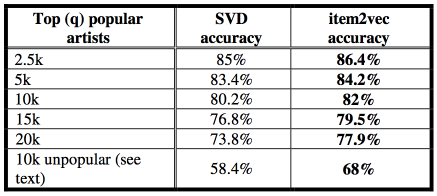
数字(原文TABLE 2を引用)でもitem2vecのほうが精度が高く、特に人気の低い(15人以下のユーザが再生した)アーティストでは約10%の差を付けている。これは、人気の高い(出現頻度の高い)アイテムについては間引かれやすく(p(discard | w)の式)、またnegative samplingの対象にもなりやすいので、人気の低いアイテムの影響が相対的に高くなったためである。

f:id:ohke:20171130143303p:plain

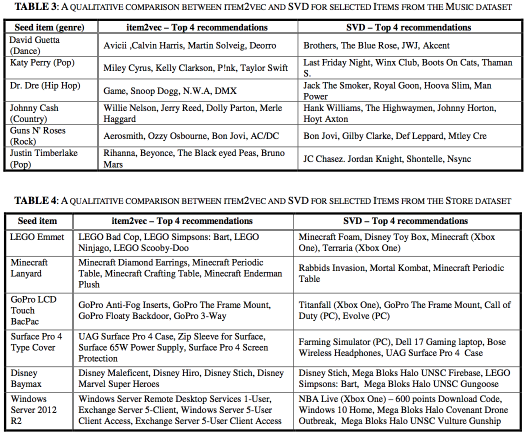
最後にMusicとStoreのそれぞれにおいて、item2vecとSVDが推薦したアイテムを比較し、いずれもitem2vecの方がより類似したアイテムを推薦していることを確認した(原文TABLE 3, TABLE 4を引用)。
特にStoreでは、「同時に購入された」という情報以外のアイテムに関する情報を捨てているにもかかわらず、類似した物が連なっていることがわかる。

f:id:ohke:20171201083136p:plain