Uplift modelingで施策が効く人を見極める

最近はお仕事でマーケティングに関わることが多いです。そんな中で、施策が効く人はどんな人？ということを特定・予測する方法を調べており、その過程で見つけたUplift modelingについてまとめました。

Uplift modeling

Uplift modelingは、施策の真の効果を推定するためのモデルで、主にマーケティングの文脈で使われます。

マーケティングの施策の実施にはコストが伴います。自社負担のクーポンや、DM・電話・訪問などの営業努力が、ここで言うコストにあたります。
そのため、施策を行って効果がある人 (反応する人と言い、ECサイトであればクーポンを使って購入する人などです) にだけ絞って行いたいものですが、これは特定するのは一筋縄ではいきません。施策によって行動変容するためです。
施策とその後の反応によって、4パターンに分けて考えられます。説得可能とあまのじゃくは行動変容していることに着目してください。難しいのは、確実だったのか説得可能だったのか (あるいは無関心だったのかあまのじゃくだったのか) が、A/Bテストだけではわからないことです。通常は同じ人に対して、施策が有り・無しの両方をテストできないからです。

パターン1. 施策の有無に関わらず、反応する人 (The Sure Things, 確実)
パターン2. もともと行うつもりではなかったが、施策によって反応を行う人 (The Persuadables, 説得可能)
パターン3. もともと行うつもりであったが、施策によって反応を行わない人 (The Do Not Disturbs, あまのじゃく)
パターン4. 施策の有無に関わらず、反応しない人 (The Lost Causes, 無関心)

こういった状況でも、施策の真の効果を推定し、説得可能を予測しようと試みるのがUplift modelingです。以下のフローで適用します。

ステップ1. 無作為抽出したターゲットに対して、A/Bテストを行う
- 訓練データの収集が目的なので、小さいサイズで試す
ステップ2. 訓練データで学習したモデルを作る
ステップ3. 得られたモデルを使い、各ターゲットについてアップリフト (uplift) を計算し、その値が大きいターゲットにのみ施策を実施する
- アップリフトが大きいほど、施策によって反応を引き出しやすいターゲットと言えます

アップリフトの計算方法は、実験群・対照群でモデルを分けるかどうかによって、バリエーションがあります (参考論文PDF) 。モデルには、ロジスティック回帰、SVMなど確率を計算できる分類モデルを使用できます。

モデルを2つに分ける場合 (2モデルアプローチ)
- 実験群と対照群のそれぞれで別のモデルを使って学習し、2つのモデルから得られた予測値の割合をアップリフトとする
単一モデルにする場合 (using class variable transformation, 1モデルアプローチ)
- 実験群と対照群からz値を計算し、z値を予測する単一モデルを学習によって獲得し、予測したz値からアップリフトを計算する

具体例: 効率的にクーポンを配布したいECサイト

大々的なクーポン配布を行おうと企画しているECサイトを想定してみます。

全体へ展開する前に、パイロット的に10人のユーザを無作為に抽出してA/Bテストしました。施策 (クーポンを配布する) の有無とその時の反応 (購入) が下表になったとします。
集計レベルでは、施策に効果が有ると言えそうです。購入に至った割合を見ると、対照群 (施策無しの群) では2割に対して、実験群 (施策有りの群) では6割となっているためです。

ユーザ	クーポン有無 (施策)	購入有無 (反応)
0	o	o
1	o	o
2	o	o
3	o	x
4	o	x
5	x	o
6	x	x
7	x	x
8	x	x
9	x	x

"大々的な"と前置きしましたが、自社負担のクーポンですので、クーポンを配布することでより効果的なユーザ (上の分類では説得可能) を特定したいと考えてます。そこで先程A/Bテストした10人のユーザに対して、最後に購入してからの日数 (経過日数) と過去1年間で購入した回数 (購入回数) を集計してみました。経過日数が長い人ほど、施策の効果がより高そうです。

ユーザ	経過日数	購入回数	クーポン有無	購入有無
0	7	1	o	o
1	10	8	o	o
2	22	7	o	o
3	3	1	o	x
4	4	5	o	x
5	7	4	x	o
6	15	2	x	x
7	18	3	x	x
8	11	9	x	x
9	4	1	x	x

この時、以下の人たちにクーポンを出すべきか否かをUplift modelingで判定してみましょう。

ユーザ	経過日数	購入回数
0'	1	1
1'	7	1
2'	1	7
3'	7	7

2モデルアプローチ

まずは2モデルアプローチから見ていきます。

施策有無 (有りならtreatment=1) によって、それぞれ異なるモデル (model_treatmentとmodel_control) で学習します。

重み (coef_) を見ると、model_treatmentとmodel_controlで正負が逆転していることがわかります
- 実験群では、経過日数の重みが正になっており、経過日数が長いほど反応しやすい
- 一方、対照群では、購入回数の重みが正で、購入回数が大きいほど反応しやすい

import pandas as pd
from sklearn.linear_model import LogisticRegression

# 訓練データ
train_df = pd.DataFrame({
    'elapsed_days': [7, 10, 22, 3, 4, 7, 15, 18, 11, 4],  # 経過日数
    'bought_count': [1, 8, 7, 1, 5, 4, 2, 3, 9, 1],  # 購入回数
    'treatment': [1, 1, 1, 1, 1, 0, 0, 0, 0, 0],  # 施策有無 (1なら有り)
    'action': [1, 1, 1, 0, 0, 1, 0, 0, 0, 0]  # 反応有無 (1なら有り)
})

# 施策有り
X_treatment = train_df[train_df['treatment'] == 1][['elapsed_days', 'bought_count']]
y_treatment = train_df[train_df['treatment'] == 1]['action']

model_treatment = LogisticRegression().fit(X_treatment, y_treatment)

for column, coef in zip(['elapsed_days', 'bought_count'], model_treatment.coef_[0]):
    print(f'{column}: {coef}')
# elapsed_days: 0.3796047271397549
# bought_count: -0.27621032600999273

# 施策無し
X_control = train_df[train_df['treatment'] == 0][['elapsed_days', 'bought_count']]
y_control = train_df[train_df['treatment'] == 0]['action']

model_control = LogisticRegression().fit(X_control, y_control)

for column, coef in zip(['elapsed_days', 'bought_count'], model_control.coef_[0]):
    print(f'{column}: {coef}')
# elapsed_days: -0.22433372044940125
# bought_count: 0.14303350531015982

次に、テストデータ4件についてアップリフトを計算します。

各モデル (model_treatmentとmodel_control) でアクションする確率を予測する
アップリフト = 施策実施時の予測反応確率 / 施策非実施時の予測反応確率で計算する

# テストデータ
test_df = pd.DataFrame({
    'elapsed_days': [1, 7, 1, 7],  # 経過日数
    'bought_count': [1, 1, 7, 7],  # 購入回数
})

y_test = pd.DataFrame()

# 施策実施時に反応する確率
y_test['prob_treatment'] = model_treatment.predict_proba(test_df[['elapsed_days', 'bought_count']])[:, 1:2].flatten()
# 施策非実施時に反応する確率
y_test['prob_control'] = model_control.predict_proba(test_df[['elapsed_days', 'bought_count']])[:, 1:2].flatten()

# アップリフトの計算
y_test['uplift'] = y_test['prob_treatment'] / y_test['prob_control']

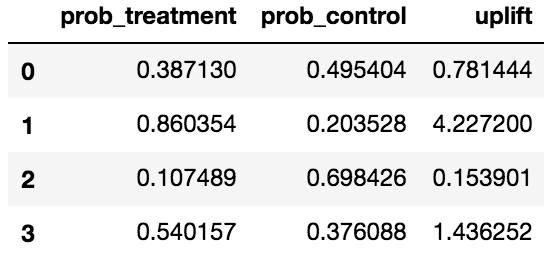
結果は下の通りとなりました。
アップリフトが最大となるのは、経過日数=7,購入回数=1のユーザ (上の表ではユーザ1') であるため、このユーザに対して施策すべし、という結論になりそうです。
一方で、経過日数=1のユーザ (上の表ではユーザ0'と2') は、1を割ってしまっているので、施策したにも関わらず、リフトするどころかマイナスになる傾向が見られます。あまのじゃくに分類されるため、こういったユーザには配布してはいけなさそうです。

2モデルアプローチは単純なのですが、それぞれ別の訓練データを使ったモデルで計算されていますので、モデルのハイパパラメータや独立変数の値域が異なっているとアップリフトも変動します。そのため、頑健な方法とは言えないです。

1モデルアプローチ

1モデルアプローチでは、まずはじめに新たにz値を導入します。

(実験群で、かつ、反応した) または (対照群で、かつ、反応しなかった) の場合に、z=1
それ以外は、z=0

実験群をT、対照群をC、反応有りをR、無しをNとしたとき、ターゲット $\vec{x}$ のアップリフトは $P(z=1 | \vec{x})$ で計算されます。

$P(z=1 | \vec{x}) = P(z=1 | T, \vec{x})P(T|\vec{x}) - P(z=1 | C, \vec{x})P(C|\vec{x}) = P(R | T, \vec{x})P(T|\vec{x}) - P(N | C, \vec{x})P(C|\vec{x})$

A/Bテストでは実験群・対照群がランダムに選択されているとする (仮定1.) と、 $P(T|\vec{x}) = P(T), P(C|\vec{x}) = P(C)$ のため、

$P(z=1|\vec{x}) = P(R|T, \vec{x})P(T) - P(N|C, \vec{x})P(C)$ .

さらに、実験群と対照群の割合が1:1とする (仮定2.) と、 $P(T)=P(C)=\frac{1}{2}$ なので、

$2P(z=1|\vec{x}) = P(R|T, \vec{x}) + P(N|C, \vec{x}) = P(R|T, \vec{x}) + 1 - P(R|C, \vec{x})$ .

最終的には下式となる。右辺の $P(z=1|\vec{x})$ をモデルで学習することで、アップリフトを予測できるようになる、ということです。

$P(R|T, \vec{x}) - P(R|C, \vec{x}) = 2P(z=1|\vec{x}) - 1$

最後にPythonで同じユーザ0'〜3'のアップリフトを学習・予測します。
z値を従属変数として1つのモデルで学習している点が、先程の2モデルアプローチと異なっていることに着目してください。

# 学習データ
X_train = train_df[['elapsed_days', 'bought_count']]
y_train = 1 - (train_df['action'] ^  train_df['treatment']) 　# z値の計算

# z値を従属変数として学習
model = LogisticRegression().fit(X_train, y_train)

for column, coef in zip(['elapsed_days', 'bought_count'], model.coef_[0]):
    print(f'{column}: {coef}')
# elapsed_days: 0.35499844965161537
# bought_count: -0.25097210802132697

y_test = pd.DataFrame()

# z値の予測
y_test['z'] = model.predict_proba(test_df[['elapsed_days', 'bought_count']])[:, 1:2].flatten()

# アップリフトの計算
y_test['uplift'] = 2 * y_test['z'] - 1

結果は下表です。同じくユーザ1' > 3' > 0' > 2'の順でアップリフトが大きいことがわかります。0を超えるユーザであれば施策によるリフトが見込めそうです。

この1モデルアプローチでは2つの仮定を置いていることに注意してください。特に2番目の仮定は、実際の適用にあたっては足かせになり得ます。アンダーサンプリングをして実験群・対照群のサンプル数を揃える、などの前処理が必要になりそうです。

参考文献

Uplift modelingの概念については、こちらの書籍を参考にしました。

AIアルゴリズムマーケティング自動化のための機械学習/経済モデル、ベストプラクティス、アーキテクチャ (impress top gear)

作者: Ilya Katsov,株式会社クイープ
出版社/メーカー: インプレス
発売日: 2018/10/22
メディア: 単行本（ソフトカバー）
この商品を含むブログを見る

また1モデルアプローチについては、こちらの論文(PDF)を参考にしました。論文中では、3. Adapting standard classification models to the uplift case using class variable transformation で説明されてます。

M. Jaskowski and S. Jaroszewicz. 
Uplift modeling for clinical trial data. 
In ICML Workshop on ClinicalData Analysis, 2012.