Python GoogleAnalyticsのデータを使って線形回帰でセッション数を予測するモデルを作る

Python 機械学習

前回の投稿で取得したGoogle Analytics(GA)のアクセスデータを使って、1日のセッション数を線形回帰で予測するモデルを作ります。

PythonでGoogle AnalyticsのデータをPostgreSQLへロードする - け日記

GAにおけるセッションは、ユーザの訪問によって開始され、サイト内でのページ遷移といった一連の操作をまとめる単位です。 セッション数=訪問数と言ってもいいかもしれません。 (以下のドキュメントが詳しいです。)

アナリティクスでのウェブ セッションの算出方法 - アナリティクス ヘルプ

準備

前回の投稿で取得したGAのデータをPostgreSQLからDataFrameに読み込みます。

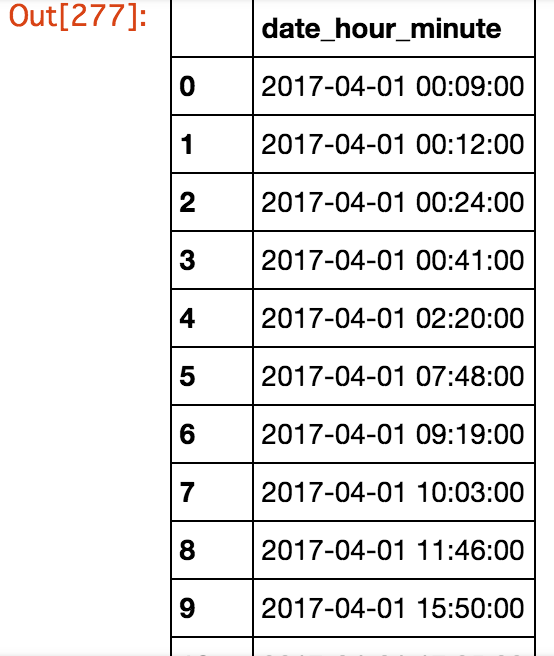
セッションの最初のアクセスのみを使うので、previous_page_pathが'(entrance)‘のレコードの時刻のみを取得しています。 (previous_page_pathは、GAのディメンションの1つであるga:previousPagePathの値を格納しています。’(entrance)‘の場合は、そのセッションで前のアクセスが無い=セッション開始を表します。)

import numpy as np
import pandas as pd
import psycopg2
import mglearn
import matplotlib.pyplot as plt
import pandas.tseries.offsets as offsets
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline

# 接続情報
pgconfig = {
    'host': 'localhost',
    'port': '5432',
    'database': 'test',
    'user': 'ohke',
    'password': 'ohke'
}

# 接続
connection = psycopg2.connect(**pgconfig)

# ga_reportテーブルからセッション最初のアクセス時刻のみをDataFrameへロード
ga_report_df = pd.read_sql(con=connection, sql="SELECT date_hour_minute FROM ga_report WHERE previous_page_path = '(entrance)';")

結果変数と説明変数

各変数を格納するDataFrameを作成します。 4/1〜6/30(13週分)の日付をインデックスとしています。

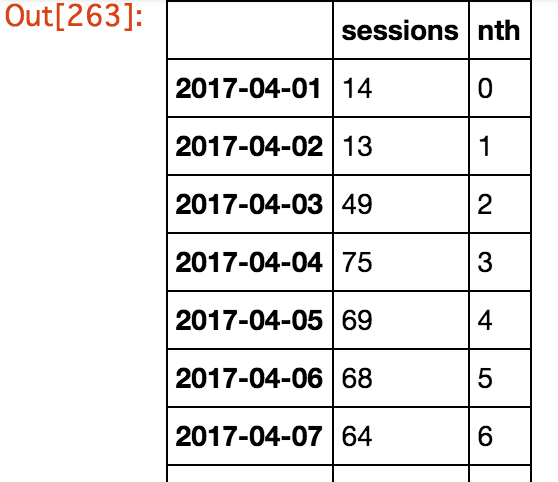
今回はある日のセッション数を予測したいので、日毎のセッション数を集計して、結果変数(sessions)としてDataFrameにセットします。

次に、4/1を0とした時に何日目なのかを表す説明変数(nth)をセットします。

# 各変数を保持するDataFrameを作成
features_df = pd.DataFrame(index=pd.date_range('2017-04-01', '2017-06-30'))

# 各日付に開始されたセッション数(結果変数)
features_df['sessions'] = ga_report_df.groupby(lambda g: ga_report_df['date_hour_minute'][g].date())['date_hour_minute'].count()

# 4/1を0として何日目か(説明変数)
features_df['nth'] = range(91)

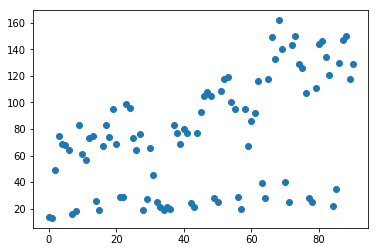
分布を可視化してみます。 マクロで見ると右肩上がりなのですが、数日おきにセッションが急激に落ち込んでいる日があります。 落ち込んでいる日は土日祝日で、言い換えると仕事中によく来訪されていることがわかります。

X = features_df['nth'].values.reshape(-1, 1)
y = features_df['sessions']
plt.plot(X, y, 'o')
plt.show()

f:id:ohke:20170713093403p:plain

線形回帰(単回帰)

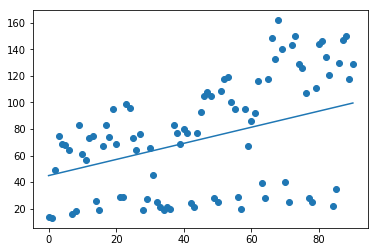
この説明変数1つ・結果変数1つのデータを使って線形回帰(単回帰)で学習・テストさせてみます。

その結果、決定係数R2(score)は学習データで0.119、テストデータで0.062と低い値となりました。

  • 学習データとテストデータを3:1(デフォルト)で分離しています
  • coefが傾き、interceptが切片になっており、この場合、傾き0.61・切片45の1次関数となります
# 学習データとテストデータに分離
X_train, X_test, y_train, y_test = train_test_split(X_learning, y_learning, random_state=0)

# 線形回帰で学習・テスト
model = LinearRegression()
model.fit(X_train, y_train)
print('coef: {}'.format(model.coef_))
print('intercept: {}'.format(model.intercept_))
print('Train score: {:.3f}'.format(model.score(X_train, y_train)))
print('Test score: {:.3f}'.format(model.score(X_test, y_test)))
# coef: [ 0.60794719]
# intercept: 44.89795159824894
# Train score: 0.119
# Test score: 0.062

f:id:ohke:20170713141234p:plain

線形回帰(重回帰)

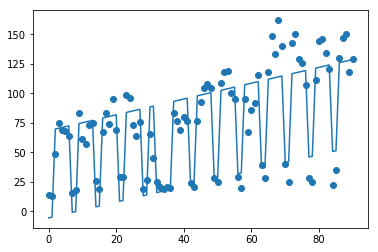
先程の学習では、何日目かという1つの特徴量だけで説明しようとしていましたので、マクロな増加傾向は掴んでいましたが、土日祝日の減少はモデルで表現できていませんでした。 そこで、土日祝日を表す説明変数(holiday)を追加して、重回帰分析を行います。

その結果、決定係数R2が学習データで0.865、テストデータで0.793と大きく改善されました。

  • 祝日の判定にはjholidayを使いました
  • 傾きcoef_は、2番目の説明変数holidayは-74で、土日祝日の場合に-74されることがわかります
    • 1番目の説明変数nthに関しては0.67と単回帰の場合とほぼ変わらず
import jholiday

# 土日祝日の場合は1(それ以外は0)となる特徴量holidayを追加
features_df['holiday'] = features_df.index.to_series().apply(lambda d: 1 if (d.date().weekday() >= 5) or (jholiday.holiday_name(date=d.date()) is not None) else 0)

# 学習データとテストデータに分離 
X = features_df[['nth', 'holiday']] # nthとholidayの2つを説明変数に指定
y = features_df['sessions']
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# 線形回帰(重回帰)で学習・テスト
model = LinearRegression() # 単回帰と同じです
model.fit(X_train, y_train)
print('coef: {}'.format(model.coef_))
print('intercept: {}'.format(model.intercept_))
print('Train score: {:.3f}'.format(model.score(X_train, y_train)))
print('Test score: {:.3f}'.format(model.score(X_test, y_test)))
# coef: [  0.67033272 -73.9860332 ] 
# intercept: 68.45651042263141
# Train score: 0.865
# Test score: 0.793

f:id:ohke:20170713142245p:plain

線形回帰(多項式回帰)

もう少し精度を上げていきます。

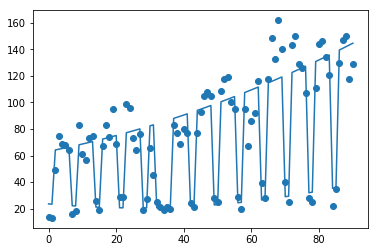
プロットされた図を見ると、緩やかにですが非線形的(放物線状)に増加していることが予想されます。 先程の特徴量を多項式にして複数次元の関数にしてみます。

ここでは次元数2で学習・テストすると、学習データで0.916、テストデータで0.832の寄与率となり、先程より少し改善されました。

  • 2変数の多項式なので、(1, nth, holiday, nth2, nth×holiday, holiday2)の6つの説明変数に拡張されます
    • したがって傾きも6つになります
  • Pipelineで多項式化、線形回帰の処理を1つにまとめています
# 多項式化、線形回帰の順に実行するPipeline
pipeline = Pipeline([
    ('polynomial', PolynomialFeatures(degree=2)),
    ('regression', LinearRegression())
])

# 学習・テスト
pipeline.fit(X_train, y_train)
print('coef: {}'.format(model.coef_))
print('intercept: {}'.format(model.intercept_))
print('Train score: {:.3f}'.format(pipeline.score(X_train, y_train)))
print('Test score: {:.3f}'.format(pipeline.score(X_test, y_test)))
# coef: [  0.00000000e+00   5.06398669e-01  -1.98226501e+01   4.43661664e-03  -7.39295022e-01  -1.98226501e+01]
# intercept: 63.2018074287475
# Train score: 0.916
# Test score: 0.832

すこーし下に凸の放物線になっていることが確認できます。

f:id:ohke:20170713200107p:plain

ちなみにPolynomialFeaturesのfit_transformメソッドで、拡張された説明変数を直接取得できます。 6つに増えていることがわかります。

PolynomialFeatures(degree=2).fit_transform(X)
# array([[  1.00000000e+00,   0.00000000e+00,   1.00000000e+00,
#           0.00000000e+00,   0.00000000e+00,   1.00000000e+00],
#        [  1.00000000e+00,   1.00000000e+00,   1.00000000e+00,
#           1.00000000e+00,   1.00000000e+00,   1.00000000e+00],
#        [  1.00000000e+00,   2.00000000e+00,   0.00000000e+00,
#           4.00000000e+00,   0.00000000e+00,   0.00000000e+00],
#        ・・・