scikit-learnで乳がんデータセットを主成分分析する
データセット
今回はUCIから提供されています乳がんデータセットを使います。 このデータセットは乳がんの診断569ケースからなります。 各ケースは検査値を含む32の値を持っており、変数の多いデータセットです。 各ケースには診断結果(良性腫瘍 or 悪性腫瘍)が付いており、これを目的変数とする分類学習となります。
Breast Cancer Wisconsin (Diagnostic) Data Set | Kaggle
このデータセット(csvファイル)をダウンロードして、ロードします。
# ライブラリのインポート import pandas as pd import matplotlib.pyplot as plt %matplotlib inline import seaborn from sklearn.preprocessing import StandardScaler from sklearn.decomposition import PCA from sklearn.pipeline import Pipeline from sklearn.linear_model import LogisticRegressionCV from sklearn.model_selection import train_test_split from sklearn.metrics import confusion_matrix # データセットのロード original_df = pd.read_csv('Breast_Cancer_Wisconsin_(Diagnostic)_Data_Set.csv') print('original_df shape: {}'.format(original_df.shape)) # original_df shape: (569, 33) # ゴミデータの削除 original_df.drop('Unnamed: 32', axis=1, inplace=True) original_df
左の列から、ID、診断結果(良性:B/悪性:M)、3列目以降は計測値等となっています。 したがって、この30列(3〜32列目)が説明変数となり
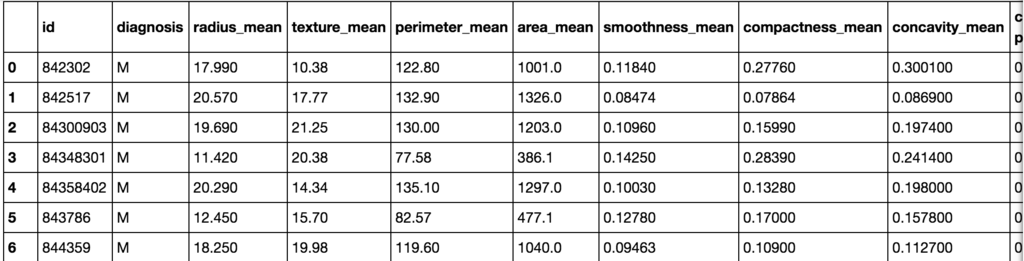
目的変数の分布を確認すると、良性:Bが357、悪性:Mが212で、悪性は全体の37%程度です。 目的変数と説明変数をそれぞれ抽出しておきます。
original_df.diagnosis.value_counts() # B 357 # M 212 # Name: diagnosis, dtype: int64 # 目的変数の抽出 y = original_df.diagnosis.apply(lambda d: 1 if d == 'M' else 0) # 説明変数の抽出 X = original_df.ix[:, 'radius_mean':]
ロジスティック回帰で学習・テスト
主成分分析で次元圧縮する前に、まずは30個の説明変数を使って、ロジスティック回帰で学習・テストさせて、基準となる精度を出しておきます。
学習データ・テストデータの分離、標準化、ロジスティック回帰(10分割交差検証)で学習・テストすると、精度97%となりました。
# 学習用とテスト用でデータを分離 X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0) # 標準化 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # ロジスティック回帰で学習 logistic = LogisticRegressionCV(cv=10, random_state=0) logistic.fit(X_train_scaled, y_train) # 検証 print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train))) print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test))) print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled)))) # Train score: 0.988 # Test score: 0.972 # Confustion matrix: # [[89 1] # [ 3 50]]
主成分分析
主成分分析する前に、現状の説明変数に相関が高そうか(次元圧縮が有効そうか)について確認します。
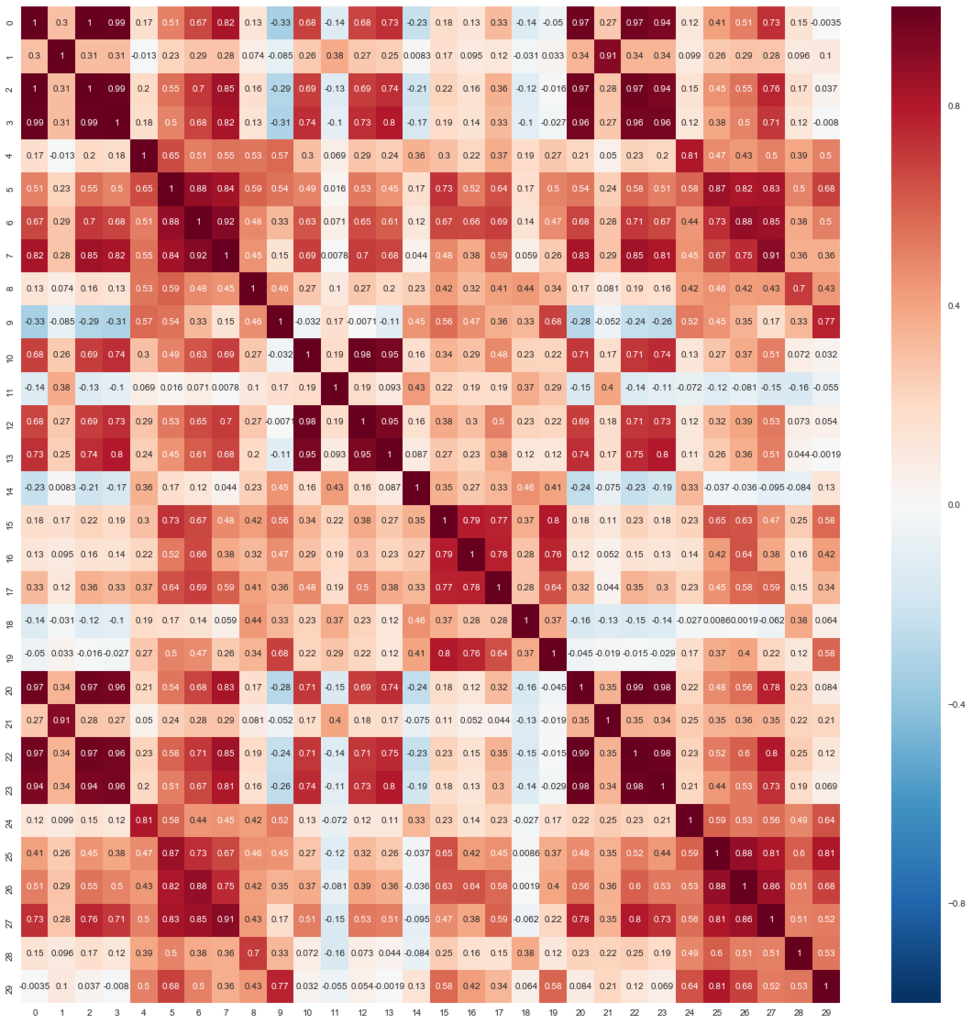
plt.figure(figsize=(20, 20)) seaborn.heatmap(pd.DataFrame(X_train_scaled).corr(), annot=True)
黒や赤のマスが幾つかあり、相関が高そうな変数が含まれることが伺えます。 次元圧縮の効果が高そうともいえます。
主成分分析は、サンプルの分散方向に着目して、新しい空間へサンプルを変換するものです。
- まず、説明変数空間内でサンプルの分散が最も大きい方向(ベクトル)を発見して、それを新しい軸(第1主成分)とします。
- 次に、新しい軸と直交し、かつ、分散が最も大きい方向(ベクトル)を発見して、またそれを新しい軸(第2主成分)とします。
- 以上を繰り返すことで、別の軸を持つ空間に、サンプルを配置し直します(射影)。
元々の次元数と同じ次元数まで繰り返すことができますが、次元圧縮する場合は途中で打ち切ります(例えば、第2主成分で打ち切った場合、2次元に圧縮できます)。 主成分分析はサンプルの分散のみに着目しているため、目的変数を必要としません。
scikit-learnではsklearn.decomposition.PCAとして提供されています。
まずは元と同じ次元数(30)にして、主成分分析をしてみて主成分の寄与率を計算します。 寄与率はその主成分の持つ分散度合い(情報量)を表します。
- 主成分分析後の次元数はn_componentsで指定します
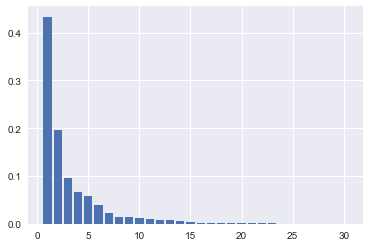
pca = PCA(n_components=30) pca.fit(X_train_scaled) plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)
寄与率は、第1主成分で43%、第2主成分で20%、・・・といった値になっており、第4主成分までの累積で80%を超えることがわかります。 主成分分析を次元圧縮に用いる場合、累積寄与率80%の主成分のみを使い、以降の主成分は切り捨てられることが多いようです。
第2主成分まで次元圧縮(30次元→2次元)して、主成分を軸として散布図にプロットしてみます。
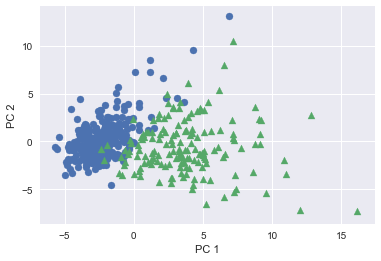
# PCA # 次元数2まで圧縮 pca = PCA(n_components=2) X_train_pca = pca.fit_transform(X_train_scaled) print('X_train_pca shape: {}'.format(X_train_pca.shape)) # X_train_pca shape: (426, 2) # 寄与率 print('explained variance ratio: {}'.format(pca.explained_variance_ratio_)) # explained variance ratio: [ 0.43315126 0.19586506] # 散布図にプロット temp = pd.DataFrame(X_train_pca) temp['Outcome'] = y_train.values b = temp[temp['Outcome'] == 0] m = temp[temp['Outcome'] == 1] plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク plt.xlabel('PC 1') # 第1主成分をx軸 plt.ylabel('PC 2') # 第2主成分をy軸
散布図を見ると、左上が良性、右下が悪性といった具合で直線で分離できそうです。
この第2主成分まで次元圧縮した説明変数を使って、学習・テストさせてみます。 標準化・次元圧縮・学習と処理が増えたので、Pipelineでまとめています。
テストデータの精度で94%となり、全ての説明変数を使った場合と比較して約3.5ポイント落としました。 30次元から2次元まで圧縮しましたが、まずまずの精度が得られているのではないでしょうか。
# パイプラインの作成 pca_pipeline = Pipeline([ ('scale', StandardScaler()), ('decomposition', PCA(n_components=2)), ('model', LogisticRegressionCV(cv=10, random_state=0)) ]) # 標準化・次元圧縮・学習 pca_pipeline.fit(X_train, y_train) # 検証 print('Train score: {:.3f}'.format(pca_pipeline.score(X_train, y_train))) print('Test score: {:.3f}'.format(pca_pipeline.score(X_test, y_test))) print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=pca_pipeline.predict(X_test)))) # Train score: 0.965 # Test score: 0.937 # Confustion matrix: # [[84 6] # [ 3 50]]
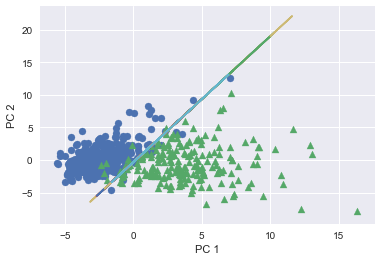
最後に決定境界をプロットしてみると、傾き1.9で切片-0.3の直線が引かれていることがわかります。
# 切片と傾き intercept = pca_pipeline.steps[2][1].intercept_ coef = pca_pipeline.steps[2][1].coef_ print('model intercept: {}'.format(intercept)) print('model coef : {}'.format(coef)) # model intercept: [-0.30694316] # model : [[ 1.78050858 -0.92218849]] # 決定境界をプロット plt.plot(X_train_scaled, -(X_train_scaled*coef[0][0] + intercept[0])/coef[0][1]) print('y = x*{} + {}'.format(-coef[0][0]/coef[0][1], -intercept[0]/coef[0][1])) # y = x*1.9307425768880175 + -0.332842107288895 # 散布図にプロット temp = pd.DataFrame(X_pca) temp['Outcome'] = y b = temp[temp['Outcome'] == 0] m = temp[temp['Outcome'] == 1] plt.scatter(x=b[0], y=b[1], marker='o') plt.scatter(x=m[0], y=m[1], marker='^') plt.xlabel('PC 1') plt.ylabel('PC 2')